Separation block

In the separation block, the instantaneous amplitude A_k(t) and the instantaneous input phase 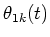$\theta_{1k}(t)$ are estimated from S_k(t) and 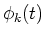$\phi _k(t)$ for the concurrent time-frequency region. This is done by the following steps, which optimize C_k,1(t) and D_k,0.

Step. 1

Let D_k,0 in Eq. (10) be any value within $-\pi/2 \leq D_{k,0} \leq \pi/2$.

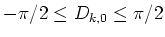Step. 2

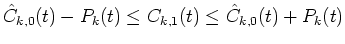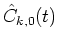Using the Kalman filter, determined the estimated region, which is $\hat{C}_{k,0}(t)-P_k(t) \leq C_{k,1}(t) \leq \hat{C}_{k,0}(t)+P_k(t)$, where $\hat{C}_{k,0}(t)$ is the estimated value and P_k(t) is the estimated error.

Step. 3

Select candidates of C_k,1(t) using the spline interpolation in the estimated error region $\hat{C}_{k,0}-P_k(t) \leq C_{k,1}(t) \leq \hat{C}_{k,0}(t)+P_k(t)$.

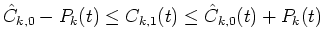Step. 4

Determine C_k,1(t) using the correlation between the instantaneous amplitudes A_k(t).

Step. 5

Repeating Steps.1 to 4, determine D_k,0 using the correlation between the instantaneous amplitudes A_k(t)

Step. 6

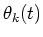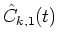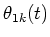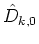Determine $\theta_k(t)$ from $\hat{C}_{k,1}(t)$ and determine $\theta_{1k}(t)$ from $\hat{D}_{k,0}$. Then, determine $\theta_{2k}(t)=\theta_k(t)+\theta_{1k}(t)$.

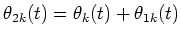Step. 7

Determine A_k(t) and B_k(t) from Eqs. (7) and (8), respectively.