Assumption and constraints of the proposed model

In this paper, it is assumed that the desired signal f₁(t) is a harmonic complex tone, consisting of the fundamental frequency F₀(t) and the harmonic components, which are multiplies of F₀(t). The proposed model segregates the desired signal from the mixed signal by constraining the temporal differentiation of the instantaneous amplitude, the instantaneous phase, and the fundamental frequency. Here, the relationship between the four regularities[Bregman1993] and the constraints concerned is shown in Table II. These constraints are defined as follows.

Constraint 1 (Gradualness of change (polynomial approximation))  

Temporal differentiations of the instantaneous amplitude A_k(t), the instantaneous phase $\theta_{1k}(t)$, and the fundamental frequency F₀(t) must be represented by an R-th-order differentiable piecewise polynomial as follows:

  

$$\frac{dA_k(t)}{dt}$$ = C_k,R(t), (9)

$$\frac{d\theta_{1k}(t)}{dt}$$ = D_k,R(t), (10)

and

 

$$\frac{dF_0(t)}{dt}$$ = E_0,R(t), (11)

where C_k,R(t), D_k,R(t), and E_0,R(t) are R-th-order differentiable piecewise polynomials. Here, A_k(t), $\theta_{1k}(t)$, and F₀(t) are represented by $A_k(t)=\int C_{k,R}(t)dt+C_{k,0}$, $\theta_{1k}(t)=\int D_{k,R}(t)dt+D_{k,0}$, and $F_0(t)=\int E_{0,R}(t)dt+E_{0,0}$, respectively. $\Box$

Constraint 2 (Harmonicity)  

F₀(t) is the fundamental frequency, and N_F0 is the number of harmonics of the highest order. The harmonic component must satisfy

$$n\cdot F_0(t), \qquad n=1,2,\cdots, N_{F_0}.$$ (12)

$\Box$

Constraint 3 (Common onset and offset)  

Suppose that $T_{\rm {S}}$ and $T_{\rm {E}}$ are the onset and offset of the fundamental component. If the signal component obtained by the k-th channel is the signal component generated by the same acoustic source (that is, harmonic components), then onset $T_{k,\rm {on}}$ and offset $T_{k,\rm {off}}$ determined by the k-th channel must coincide with $T_{\rm {S}}$ and $T_{\rm {E}}$ respectively. That is, the differences in onset and offset must satisfy

$$\vert T_{\rm {S}}-T_{k,\rm {on}}\vert\leq \Delta T_{\rm {S}}$$ (13)

and

$$\vert T_{\rm {E}}-T_{k,\rm {off}}\vert\leq \Delta T_{\rm {E}},$$ (14)

respectively. $\Box$

Constraint 4 (Gradualness of change (smoothness))  

Suppose that the amplitude envelope A_k(t) is defined in the closed-duration [t_a,t_b] and satisfies constraint 1. If A_k(t) is as smooth as possible, then the following integral must be minimized:

$$\sigma=\int_{t_a}^{t_b} [A_k^{(R+1)}(t)]^2dt,$$ (15)

where A_k^(R+1)(t) is determined by C_k,R(t) in constraint 1. $\Box$

Constraint 5 (Correlation between the instantaneous amplitudes tex2html_wrap_inline$A_k(t)$)   The normalized amplitude envelope of the output of the k-th channel must approximate that of the $\ell$-th channel as follows:

$$\frac{A_k(t)}{\Vert A_k(t)\Vert}\approx \frac{A_{\ell}(t)}{\Vert A_\ell(t)\Vert},\qquad k\not=\ell,$$ (16)

where $\Vert\cdot\Vert$ is the norm symbol. The norm of A_k(t), determined by $\Vert A_k(t)\Vert$, is determined as $\Vert A_k(t)\Vert=\sqrt{\int_0^t \vert A_k(\tau)\vert^2d\tau}$. $\Box$

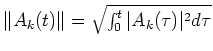Substituting constraint (9) in Eq. (7), we get the linear differential equation of the instantaneous input phase difference $\theta_k(t)$. By solving this linear differential equation, we can determine $\theta_k(t)$ as follows.

Lemma 1   From constraint 1, a general solution of the input phase $\theta_k(t)$ is determined by

$$\theta_k(t)=\arctan\left(\frac{S_k(t)\sin(\phi_k(t)-\theta_{1k}(t))}{S_k(t)\cos(\phi_k(t)-\theta_{1k}(t))+C_k(t)}\right),$$ (17)

where $C_k(t)=-\int C_{k,R}(t)dt-C_{k,0}=-A_k(t)$. The C_k(t) is called the ``undetermined function''.

(Proof) See appendix A. $\Box$

From Lemma 1, if C_k(t) is determined, then $\theta_k(t)$ is uniquely determined by the above equation. Moreover, if D_k,R(t) is determined, then the two instantaneous input phases can be determined using $\theta_k(t)$ and D_k,R(t). Therefore, if the two R-th-order polynomials C_k,R(t) and D_k,R(t) are determined as some kind of optimization problem, the two instantaneous amplitudes and the two instantaneous phases can be estimated. Although it is possible to estimate the coefficients C_k,r(t) and D_k,r(t), $r=0,2,=\cdots, R$, there is a problem that the computational cost of estimating two polynomials increases greatly.

In this paper, in order to reduce the computational cost, we assumed that C_k,R(t) is a linear (R=1) polynomial ( dA_k(t)/dt=C_k,1(t)) and D_k,R(t) is zero ( $d\theta_{1k}(t)/dt=D_{k,0}=0$) in constraint 1. In this assumption, the instantaneous amplitude A_k(t) which can be allowed to undergo a temporal change in region, constrains the second order polynomial ( $A_k(t)=\int C_{k,1}(t)dt+C_{k,0}$). Moreover, the instantaneous phase $\theta_{1k}(t)$, which is constrained (i.e. $\theta_{1k}(t)=D_{k,0}$), cannot be allowed to temporarily change. Here, if the number of channels K is very large, each frequency of the signal component that passed through the channel approximately coincides with the center frequency of each channel. Even if the above condition is false, its frequency difference can be represented by D_k,0.

This paper solves the problem of segregating the desired signal f₁(t) from the mixed signal, in which noise f₂(t) is added to the localized f₁(t), under the above assumption.