The system of considering the Kalman filtering problem is a linear stochastic state-observation description as follows:
In this system, mean and variance with
![]() ,
,
![]() ,
and
,
and
![]() are known.
And
are known.
And
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() are known matrices.
The Kalman filtering problem is to determine the minimum variance requirement
are known matrices.
The Kalman filtering problem is to determine the minimum variance requirement
![]() from the observed
from the observed
![]() ,
,
![]() as follows.
as follows.
| (56) |
It is calculated by sequentially performing the following:[Brown and Hwang1992].
| (57) | |||
| (58) |
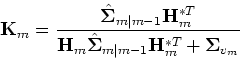 |
(59) |
| (60) | |||
| (61) |
| (62) |
 |
 |
 |
 |
 |
 |
 |
| Symbol | Definition |
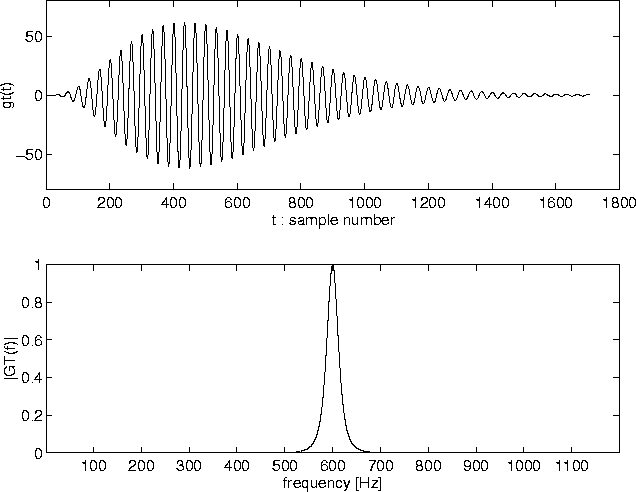
| Sk(t) | instantaneous amplitude |
| instantaneous output phase | |
| Ak(t), Bk(t) | instantaneous amplitude |
|
|
instantaneous input phases |
|
|
input phase difference |
| F0(t) | Fundamental frequency |
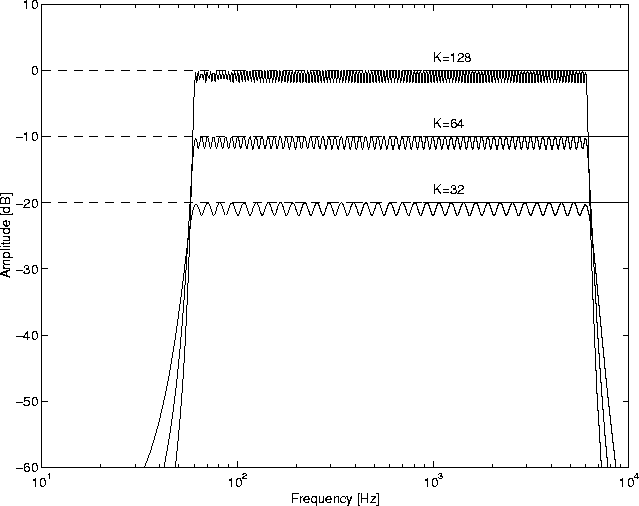
| Ck,R(t), Dk,R(t), | R-th-order polynomial |
|
|
|
| Ck(t) | undetermined function |
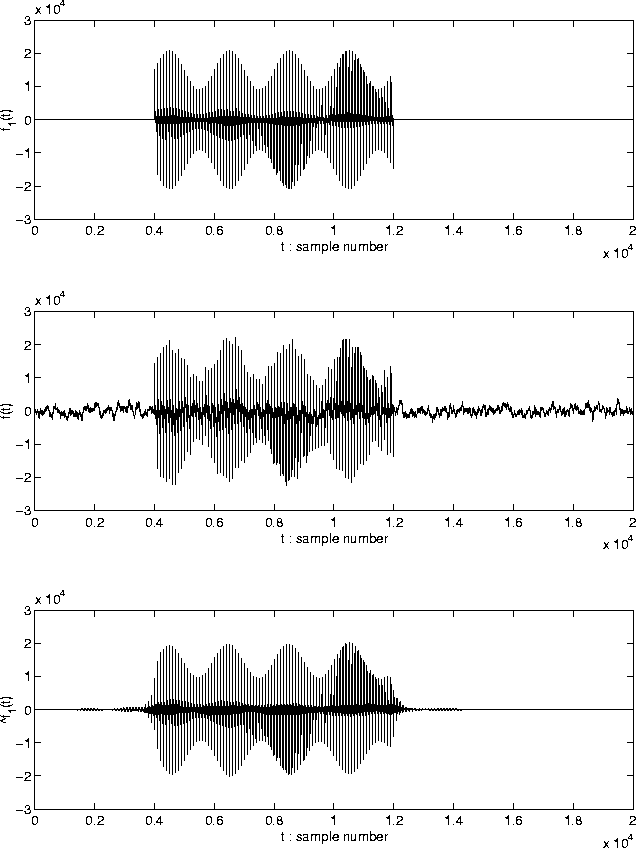
| Heuristic regularity (Bregman, 1993) | Constraint |
| (i) Unrelated sounds seldom start or stop at exactly | Synchronous of onset and offset |
| the same time. | |
| (ii) Gradualness of change. | Gradualness of change |
| (a) A single sound tends to change its properties | (piecewise-differentiable polynomial |
| smoothly and slowly. | approximation and smoothness) |
| (b) A sequence of sounds from the same source | (piecewise-differentiable polynomial |
| tends to change its properties slowly. | approximation and smoothness) |
| (iii) When a body vibrates with a repetitive period, | Harmonicity |
| this vibrations give rise to an acoustic pattern | |
| in which the frequency components are | |
| multiples of a common fundamental. | |
| (iv) Many changes that take place in an acoustic | Correlation between the |
| event will affect all the components of the | instantaneous amplitudes |
| resulting sound in the same way and at | |
| the same time. |