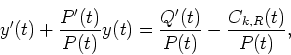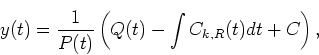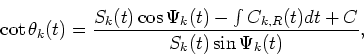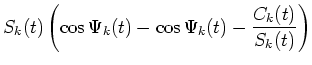Next: Appendix B: Wavelet transform
Up: Bibliography
Previous: Bibliography
Let
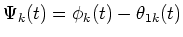 .
Rearranging Eq. (7), we obtain
.
Rearranging Eq. (7), we obtain
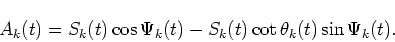 |
(36) |
Differentiating both terms in t in the above equation, we obtain
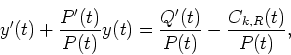 |
(37) |
where
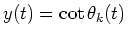 ,
,
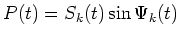 ,
and
,
and
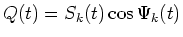 .
Since the above equation is a linear differential equation, a general solution y(t) is determined by
.
Since the above equation is a linear differential equation, a general solution y(t) is determined by
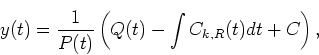 |
(38) |
where C is an undermined coefficient.
Hence, from
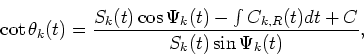 |
(39) |
we obtain
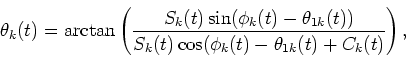 |
(40) |
where
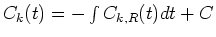 .
On the other hand, applying Eq. (36) into Eq. (40), we obtain
.
On the other hand, applying Eq. (36) into Eq. (40), we obtain
| Ak(t) |
= |
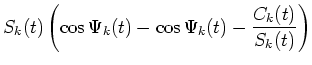 |
|
| |
= |
-Ck(t). |
(41) |
Considering that
C=-Ck,0, that is the same result as integrating Eq. (9).



Next: Appendix B: Wavelet transform
Up: Bibliography
Previous: Bibliography
Masashi Unoki
2000-11-07
![]() .
Rearranging Eq. (7), we obtain
.
Rearranging Eq. (7), we obtain