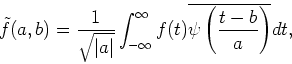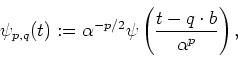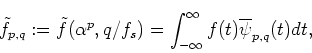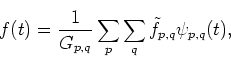Next: Appendix C: Proof of
Up: Bibliography
Previous: Appendix A: Proof of
First, we summarize the wavelet transform and the inverse wavelet transform[Chui1992] for designing a constant Q filterbank.
The integral wavelet transform for f(t) is defined by
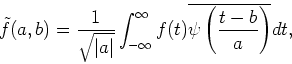 |
(42) |
where a is the ``scale parameter,'' b is the ``shift parameter,''
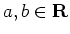 with
with 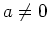 ,
and
,
and
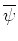 is the conjugate of
is the conjugate of 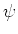 .
The integral basis function is
.
The integral basis function is 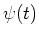 scale-transformed by parameter a and shifted by parameter b.
The selection of
scale-transformed by parameter a and shifted by parameter b.
The selection of 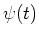 allows much mathematical freedom; however, in general,
allows much mathematical freedom; however, in general, 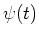 is determined to be an integrable function that satisfies the following ``admissibility condition'':
is determined to be an integrable function that satisfies the following ``admissibility condition'':
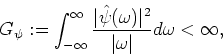 |
(43) |
where
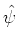 is the Fourier transform of
is the Fourier transform of 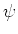 ,
It follows that
,
It follows that
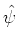 is a continuous function, so that the finiteness of
is a continuous function, so that the finiteness of 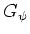 in Eq. (43) implies that
in Eq. (43) implies that
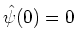 ,
or equivalently,
,
or equivalently,
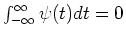 .
If the above equation is satisfied,
.
If the above equation is satisfied, 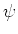 is called a ``basic wavelet,'' and a unique inverse transform exists as follows:
is called a ``basic wavelet,'' and a unique inverse transform exists as follows:
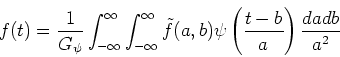 |
(44) |
Since the analyzing wavelet 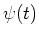 in Eq. (20) approximately satisfies the admissibility condition because
in Eq. (20) approximately satisfies the admissibility condition because
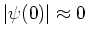 ,
it can be considered that this analyzing wavelet is the basic wavelet.
,
it can be considered that this analyzing wavelet is the basic wavelet.
Equations. (42)-(44) are a continuous wavelet transform.
The discrete wavelet transform corresponding to these equations is represented by
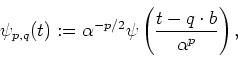 |
(45) |
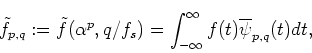 |
(46) |
and
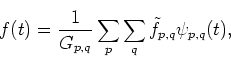 |
(47) |
where p and q are integer parameters.



Next: Appendix C: Proof of
Up: Bibliography
Previous: Appendix A: Proof of
Masashi Unoki
2000-11-07