Auditory sound segregation model

 

Table: Constraints corresponding to Bregman's psychoacoustical heuristic regularities.

  center tabularlll Regularity (Bregman, 1993) & Constraint (Unoki and Akagi,& 1999)
(i) Unrelated sounds seldom start or stop at exactly & Synchronism of onset/offset & tex2html_wrap_inline$|T_S-T_k,on| T_S$
the same time (common onset/offset)& & tex2html_wrap_inline$|T_E-T_k,off| T_E$
(ii) Gradualness of change & (a) Slowness (piecewise- & tex2html_wrap_inline$dA_k(t)/dt=C_k,R(t)$
(a) A single sound tends to change its properties & differentiable polynomial & tex2html_wrap_inline$d_1k(t)/dt=D_k,R(t)$
smoothly and slowly & approximation) & tex2html_wrap_inline$dF_0(t)/dt=E_0,R(t)$
(b) A sequence of sounds from the same source & (b) Smoothness & tex2html_wrap_inline$_A=_t_a^t_b [A_k^(R+1)(t)]^2dt $
tends to change its properties slowly & (Spline interpolation)& tex2html_wrap_inline$_=_t_a^t_b [_1k^(R+1)(t)]^2dt $
(iii) When a body vibrates with a repetitive period, & Multiples of the repetitive &
these vibrations give rise to an acoustic pattern & fundamental frequency & tex2html_wrap_inline$nF_0(t),         n=1,2,, N_F_0$
in which the frequency components are multiples & &
of a common fundamental (harmonicity)& &
(iv) Many changes that take place in an acoustic event & Correlation between the &
will affect all the components of the resulting & instantaneous amplitudes & tex2html_wrap_inline$A_k(t)||A_k(t)|| A_(t)||A_(t)||$, tex2html_wrap_inline$        k=$
sound in the same way and at the same time & &
 

 

Table: Constraints corresponding to Bregman's psychoacoustical heuristic regularities.

Regularity (Bregman, 1993)	Constraint (Unoki and Akagi,	1999)
(i) Unrelated sounds seldom start or stop at exactly	Synchronism of onset/offset	$\vert T_{\rm{S}}-T_{k,\rm{on}}\vert \leq \Delta T_{\rm{S}}$
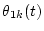the same time (common onset/offset)		$\vert T_{\rm{E}}-T_{k,\rm{off}}\vert \leq \Delta T_{\rm{E}}$
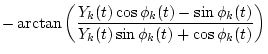(ii) Gradualness of change	(a) Slowness (piecewise-	dAk(t)/dt=Ck,R(t)
(a) A single sound tends to change its properties	differentiable polynomial	$d\theta_{1k}(t)/dt=D_{k,R}(t)$
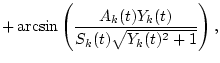smoothly and slowly	approximation)	dF0(t)/dt=E0,R(t)
(b) A sequence of sounds from the same source	(b) Smoothness	$\sigma_A=\int_{t_a}^{t_b} [A_k^{(R+1)}(t)]^2dt \Rightarrow \min$
tends to change its properties slowly	(Spline interpolation)	$\sigma_\theta=\int_{t_a}^{t_b} [\theta_{1k}^{(R+1)}(t)]^2dt \Rightarrow \min$
(iii) When a body vibrates with a repetitive period,	Multiples of the repetitive
these vibrations give rise to an acoustic pattern	fundamental frequency	$n\times F_0(t), \qquad n=1,2,\cdots, N_{F_0}$
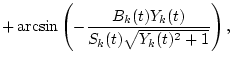in which the frequency components are multiples
of a common fundamental (harmonicity)
(iv) Many changes that take place in an acoustic event	Correlation between the
will affect all the components of the resulting	instantaneous amplitudes	$\frac{A_k(t)}{\Vert A_k(t)\Vert} \approx \frac{A_{\ell}(t)}{\Vert A_\ell(t)\Vert}$, $\qquad k\not=\ell$
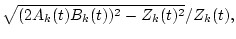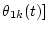sound in the same way and at the same time

  

Figure: Auditory sound segregation model.

In this paper, it is assumed that the desired signal f₁(t) is a harmonic complex tone, where F₀(t) is the fundamental frequency. The proposed model segregates the desired signal from the mixed signal by constraining the temporal differentiation of A_k(t), $\theta_{1k}(t)$, and F₀(t).

The proposed model is composed of four blocks: an auditory-motivated filterbank, an F₀ estimation block, a separation block, and a grouping block, as shown in Fig. . Constraints used in this model are shown in Table 1.