F₀ estimation block

  

Figure: Temporal variation of the fundamental frequency.

The F₀ estimation block determines the fundamental frequency of f₁(t). This block is implemented as the Comb filtering on an amplitude spectrogram S_k(t)s [Unoki and Akagi1998].

In this block, the Comb filter is defined by

$${\rm{Comb}}(k,l)=\left\{\begin{array}{ll} \frac{(\alpha+1)}{(... ...uad 1\leq n \leq N\\ 0, & \mbox{otherwise} \end{array}\right.$$ (10)

where k and l are indices, $\omega_k$ and $\omega_l$ are the center frequencies in channels, and N is the number of harmonics of the highest order. Then, $\hat{l}$, which corresponds to the channel containing the fundamental wave, is determined by

$$\hat{l}(t;L_F) = \mathop{\arg \max}_{l\leq L_F}\sum_{k=1}^K {\rm{Comb}}(k,l)S_k(t),$$ (11)

where L_F is the upper-limited search region of l. The estimated F₀(t) is determined by

$$F_0(t)=\mathop{\min}_{L_F} {\rm{std}}(\omega_{\hat{l}}/2\pi).$$ (12)

In this paper, we let the parameters be N=10 and $K/4 \leq L_F \leq K/2$.

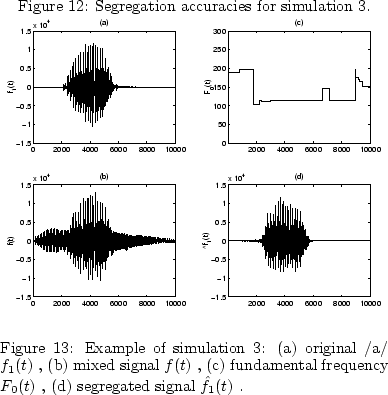
Since the number of channels in X_k(t) is finite, the estimated F₀(t) takes a discrete value as shown in Fig. . In addition, the fluctuation of F₀(t) has a staircase shape and the temporal differentiation of F₀(t) is zero at any segment. Therefore, this paper assumes that E_0,R(t)=0 in constraint (ii) of Table 1 for a segment. Let the length of the above segment be T_h-T_h-1, where T_h is the continuous point of F₀(t).