EMCによる解析

を K個 の正規直交基底 により次式で近似することを考える．

 

ただし，

とする． 従来の固有空間法では， を と元パターン との平均2乗誤差を最小にするように選ぶが，提案するEMCで は，理想的な近似パターンを各クラスの平均パターンと考え， を と各クラスの平均パターン との平均2乗誤差 を最小 にするように選ぶ．

 

これにより求められたK個の を使って展開した結果から得られるK次元 ベクトル が解析に用いる次元圧縮された特徴ベクトルとなる． なお， のk番目の要素は次式から得られる．

 

この は次式の固有値問題を解くことにより求まる （節）．

 

ただし，

 

とする． ここで式()の左から を掛け，式 ()を使うと，

 

が得られる． ここで と は全クラス集合Fにおける の級間分散と 級内分散である． 式(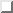)は固有値 が級間分散と級内分散の差に等しい ことを表している． ここで級間分散と級内分散の差をクラス集合Fの特徴の分離度（以後，これ を分離度1と呼ぶ）とみなすと， が大きいほどそれに対応する はFの特徴を良く表 す固有ベクトルと考えられる．