（証明）
式(
)に式()を代入すると，
を得る． ただし，
とする． ここで，正規直交条件より，
を得る．
ここで，式()()()より，
を得る．
式(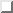)の第一項は 
の選び方に独立であるから，式
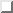()を最小にする問題は次の制約条件つき最適化問題と同等である．
Find that maximizes
subject to the constraints
さらに，Lagrangeの未定係数法よりこの制約条件つき最適化問題は 次の最適化問題と同等である．
Find 
that maximizes
ただし，Lagrange係数を 
とする．
ここで式(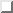)の極値では，
が成り立つ． ただし，
とする．
ここで，Sは実対称行列なので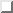，式()より式
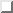()の固有値問題を得る．
また，式(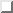)を最大にするには， 
を大きい順にK個
選ぶこととなる． 
