MDAは級間分散と級内分散の比を最大にするような線形変換を求める手法であ
る.
しかし,MDAを行うには級内変動行列が正定値対称行列でなければならない.
これはMDAを適用するベクトルの次元数をLとすると, ![]() を満た
すことと同等である.
ただし,|F|はFの要素数を表す.
そこでLを小さくするために,本研究ではPCAを行い次元圧縮された特徴ベク
トルに対してMDAを行う.
を満た
すことと同等である.
ただし,|F|はFの要素数を表す.
そこでLを小さくするために,本研究ではPCAを行い次元圧縮された特徴ベク
トルに対してMDAを行う.
![]() のPCA後のL次元特徴ベクトルを
のPCA後のL次元特徴ベクトルを
![]() とする.
なお,本研究ではL=M-|F|に設定した.
ここでMDAによってI次元(
とする.
なお,本研究ではL=M-|F|に設定した.
ここでMDAによってI次元( ![]() )に次元圧縮される特徴ベクトルの
i番目の要素は,以下のようにL次元係数ベクトル
)に次元圧縮される特徴ベクトルの
i番目の要素は,以下のようにL次元係数ベクトル ![]()
![]()
![]() と
と ![]() との線形結
合で表される.
との線形結
合で表される.
ここで ![]() と
と ![]() を
を ![]() の級間分散と級内分散とする.
そして,
の級間分散と級内分散とする.
そして,
を最大かつ ![]() の各i成分が互いに無相関となるように
の各i成分が互いに無相関となるように ![]() を
選ぶ.
そして,式(
を
選ぶ.
そして,式(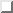 )により得られるI次元ベクトル
)により得られるI次元ベクトル ![]() を用い解析を行う.
を用い解析を行う.
![]() は次式の一般固有値問題を解くことにより求まる[10].
は次式の一般固有値問題を解くことにより求まる[10].
ただし,
とする.
このBは級間変動行列,Wは級内変動行列を表す.
ここで式(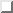 )の左から
)の左から ![]() を掛け,式
(
を掛け,式
(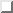 )を使うと,
)を使うと, ![]() は式(
は式(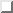 )の
)の ![]() と一致
する.
この
と一致
する.
この ![]() をクラス集合Fの特徴の分離度(以後,これを分離度2と呼ぶ)
とみなすと,
をクラス集合Fの特徴の分離度(以後,これを分離度2と呼ぶ)
とみなすと, ![]() が大きいほど対応する
が大きいほど対応する ![]() はFの特徴を良く表
す固有ベクトルと考えられる.
はFの特徴を良く表
す固有ベクトルと考えられる.