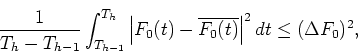Determination of the fundamental frequency

In this paper, the fundamental frequency of the complex tones is estimated using TEMPO (a method of time-domain excitation extraction based on a minimum perturbation operator) [Kawahara1997].

Next, consider the constraint of gradualness of change in Eq. (11) for the estimated fundamental frequency F₀(t). The estimated F₀(t) can take continuous values. However, since the number of channels in the auditory-motivated filterbank is finite, the center frequencies of the auditory-motivated filterbank cannot take continuous values. Therefore, it is difficult to deal with continuous temporal variation of F₀(t). In this paper, we assume that E_0,R(t)=0 in Eq.(11) for a small segment, means that F₀(t) is constant in a small segment. Here, the above small segment is determined using the following equation, as the duration for which the temporal variation of F₀(t) has the same variance as F₀(t).

$$\frac{1}{T_{h}-T_{h-1}}\int_{T_{h-1}}^{T_h} \left\vert F_0(t)-\overline{F_0(t)}\right\vert^2 dt \leq (\Delta F_0)^2,$$ (24)

where the length of the small segment is T_h-T_h-1 and $\Delta (F_0)^2$ is the variance of F₀(t). In this paper, $\Delta F_0=1$ Hz.

The relationship between F₀(t) and the small segments using constraint 1 is shown in Fig. 6. For F₀(t), as shown by the dotted line in Fig. 6, segregated duration (F₀(t) duration) is applied to small segments from Eq. (24). The number of split segments is H-1.