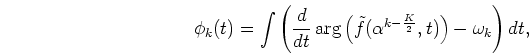Next: Biography
Up: No Title
Previous: Bibliography
The wavelet transform in Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) is a complex
representation for the output of analytic filter in Eq.
(
) is a complex
representation for the output of analytic filter in Eq.
(![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ).
).
| Xk(t) |
= |
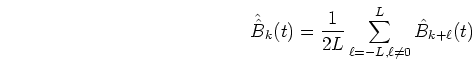 |
|
| |
:= |
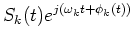 |
(32) |
Representing an absolute value for both terms, we obtain
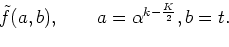 |
(33) |
Similarly, comparing the phase terms between Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and
(
) and
(![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ), we obtain
), we obtain
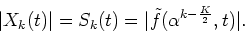 |
(34) |
Since the phase spectrum
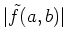 is represented by
is represented by
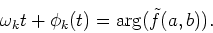 |
(35) |
it becomes a periodical ramp function within
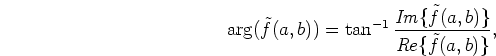 Differentiating both terms in Eq. (
Differentiating both terms in Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ), it becomes
), it becomes
After clearing, we obtain
Hence, the output phase 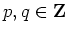 is represented by
is represented by



Next: Biography
Up: No Title
Previous: Bibliography
Masashi Unoki
2000-10-26
![]() ) is a complex
representation for the output of analytic filter in Eq.
(
) is a complex
representation for the output of analytic filter in Eq.
(![]() ).
).
![]() ) and
(
) and
(![]() ), we obtain
), we obtain
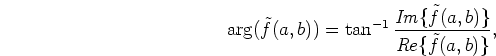 Differentiating both terms in Eq. (
Differentiating both terms in Eq. (