


Next: Characteristic of the gammatone
Up: Wavelet filterbank with the
Previous: Wavelet filterbank with the
Firstly, to design a wavelet filterbank, the wavelet transform and the
inverse wavelet transform are summarized as follows.
The integral wavelet transform for f(t) is defined by
 |
(9) |
where a is the ``scale parameter,'' b is the ``shift parameter,''
and
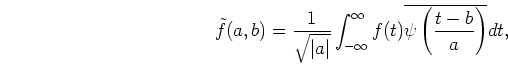 is the conjugate of
is the conjugate of 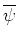 .
The integral basis function is
.
The integral basis function is 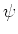 scale-transformed by
the parameter a and is shifted by the parameter b.
The selection of
scale-transformed by
the parameter a and is shifted by the parameter b.
The selection of 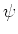 allows much mathematically freedom; however,
in general,
allows much mathematically freedom; however,
in general, 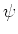 is determined to be an integrable function
satisfied by the following admissibility condition [20]:
is determined to be an integrable function
satisfied by the following admissibility condition [20]:
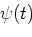 |
(10) |
where
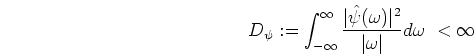 is the Fourier transform of
is the Fourier transform of 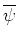 .
If the above equation is satisfied,
.
If the above equation is satisfied, 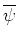 is called a ``basic
wavelet,'' and the inverse transform exists uniquely as follows[20]:
is called a ``basic
wavelet,'' and the inverse transform exists uniquely as follows[20]:
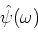 |
(11) |
If 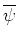 is absolutely integrable function, the admissibility
condition implies
is absolutely integrable function, the admissibility
condition implies
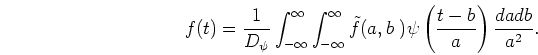 .
.
If the basic wavelet is defined on a complex plane, it is
possible that the wavelet transform is represented by the amplitude
spectrum
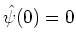 and the phase spectrum
and the phase spectrum
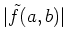 as follows [21]:
as follows [21]:
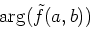 |
(12) |
To construct an auditory filterbank simulating the auditory system,
we selected as a basic wavelet the gammatone filter to simulate
the response of the basilar membrane.



Next: Characteristic of the gammatone
Up: Wavelet filterbank with the
Previous: Wavelet filterbank with the
Masashi Unoki
2000-10-26
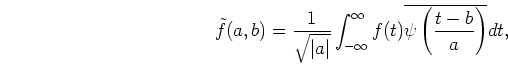 is the conjugate of
is the conjugate of 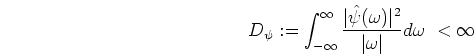 is the Fourier transform of
is the Fourier transform of 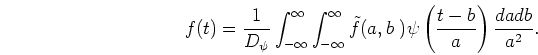 .
.
![]() and the phase spectrum
and the phase spectrum
![]() as follows [21]:
as follows [21]: