


Next: Wavelet filterbank
Up: Wavelet filterbank with the
Previous: Definition of the wavelet
The gammatone filter is an auditory filter designed by
Patterson[22], and is known to simulate well the
response of the basilar membrane.
The impulse response of the gammatone filter is defined by
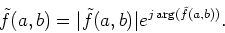 |
(13) |
where
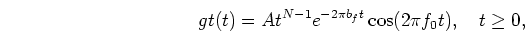 is the amplitude term represented by
the Gamma distribution and f0 is the center frequency.
The amplitude characteristics of the gammatone filter are
represented, approximately, by
is the amplitude term represented by
the Gamma distribution and f0 is the center frequency.
The amplitude characteristics of the gammatone filter are
represented, approximately, by
![\begin{displaymath}GT(f) \approx \left[1+\frac{j(f-f_0)}{b_f}\right]^{-N},\quad
0<f<\infty,
\end{displaymath}](img32.gif) |
(14) |
where GT(f) is the Fourier transform of gt(t) and represents
bandpass filtering with a center frequency of f0.
Characteristics of impulse response and amplitude of the gammatone
filter are shown in Fig. ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) .
Since it is clear from this figure that
.
Since it is clear from this figure that
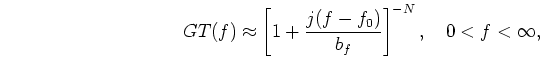 ,
the
gammatone filter satisfies approximately the admissibility condition,
meaning it can be used sufficiently as the basic wavelet.
,
the
gammatone filter satisfies approximately the admissibility condition,
meaning it can be used sufficiently as the basic wavelet.
Masashi Unoki
2000-10-26
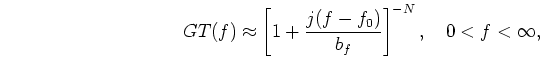 ,
the
gammatone filter satisfies approximately the admissibility condition,
meaning it can be used sufficiently as the basic wavelet.
,
the
gammatone filter satisfies approximately the admissibility condition,
meaning it can be used sufficiently as the basic wavelet.