


Next: Wavelet filterbank with the
Up: No Title
Previous: Introduction
In this paper, the problem of segregating two acoustic sources is
defined as ``the segregation of original signal components from a
noise-added signal, where mixed signal is composed of two signals
generated by two acoustic sources.''
This problem is formulated as follows.
Firstly, we can observe only the signal f(t):
where f1(t) and f2(t) are the original acoustic signals.
The observed signal is decomposed into its frequency components by an
auditory filterbank as shown in Fig. ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) .
Secondly, outputs of the k-th channel, which correspond to f1(t)and f2(t), are assumed to be
.
Secondly, outputs of the k-th channel, which correspond to f1(t)and f2(t), are assumed to be
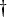 |
(2) |
and
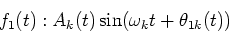 |
(3) |
respectively.
Here, 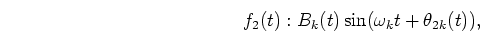 is a center frequency of the auditory filter and
is a center frequency of the auditory filter and
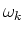 and
and
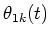 are input phases of f1(t)and f2(t), respectively.
Since the output of the k-th channel Xk(t) is the sum of Eqs.
(
are input phases of f1(t)and f2(t), respectively.
Since the output of the k-th channel Xk(t) is the sum of Eqs.
(![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ), then it is represented by
), then it is represented by
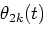 |
(4) |
Here,
| Sk(t) |
| |
= |
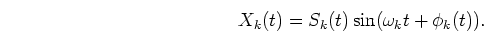 |
(5) |
and
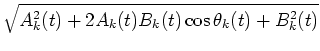 |
| |
= |
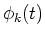 |
(6) |
where
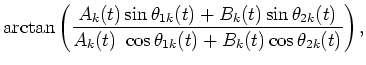 and
and
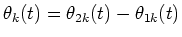 .
Since the amplitude envelope Sk(t) and the input phase are
observable and if the input
phases
.
Since the amplitude envelope Sk(t) and the input phase are
observable and if the input
phases
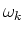 and
and
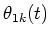 are determined, the
amplitude envelopes Ak(t) and Bk(t) can be determined by
are determined, the
amplitude envelopes Ak(t) and Bk(t) can be determined by
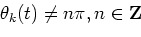 |
(7) |
and
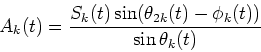 |
(8) |
respectively.
Finally, for each auditory filter, determining of Ak(t) and Bk(t),
f1(t) and f2(t) are reconstructed from Eqs.
(![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) synthesizing each frequency
components.
Here,
) synthesizing each frequency
components.
Here,
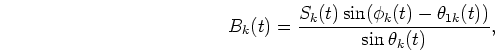 and
and
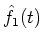 are the reconstructed f1(t)and f2(t), respectively.
are the reconstructed f1(t)and f2(t), respectively.
In this paper, the analysis synthesis system (filterbank) as shown in
Fig. ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) is constructed using the wavelet transform.
We assume that
is constructed using the wavelet transform.
We assume that
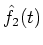 ,
,
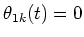 ,
and that f1(t) is an amplitude modulation
signal.
We also assume that a center frequency of analytic filter
matches a center frequency of f1(t), and that f2(t) is a
bandpassed random noise which the center frequency is the same as
f1(t).
We will also consider the problem of segregating two acoustic
sources in which the localized f1(t) is added to f2(t).
,
and that f1(t) is an amplitude modulation
signal.
We also assume that a center frequency of analytic filter
matches a center frequency of f1(t), and that f2(t) is a
bandpassed random noise which the center frequency is the same as
f1(t).
We will also consider the problem of segregating two acoustic
sources in which the localized f1(t) is added to f2(t).



Next: Wavelet filterbank with the
Up: No Title
Previous: Introduction
Masashi Unoki
2000-10-26
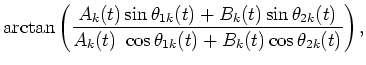 and
and
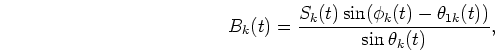 and
and
![]() is constructed using the wavelet transform.
We assume that
is constructed using the wavelet transform.
We assume that
![]() ,
,
![]() ,
and that f1(t) is an amplitude modulation
signal.
We also assume that a center frequency of analytic filter
matches a center frequency of f1(t), and that f2(t) is a
bandpassed random noise which the center frequency is the same as
f1(t).
We will also consider the problem of segregating two acoustic
sources in which the localized f1(t) is added to f2(t).
,
and that f1(t) is an amplitude modulation
signal.
We also assume that a center frequency of analytic filter
matches a center frequency of f1(t), and that f2(t) is a
bandpassed random noise which the center frequency is the same as
f1(t).
We will also consider the problem of segregating two acoustic
sources in which the localized f1(t) is added to f2(t).