Input phase
![]() can be determined by applying three
physical constraints: (i) gradualness of change, (ii) continuity
(temporal proximity), and (iii) changes in an acoustic event.
In particular, constraints (i) and (iii) are regularity (2) and (4)
proposed by Bregman.
can be determined by applying three
physical constraints: (i) gradualness of change, (ii) continuity
(temporal proximity), and (iii) changes in an acoustic event.
In particular, constraints (i) and (iii) are regularity (2) and (4)
proposed by Bregman.
We will first apply regularity (i). This regularity states that ``a single sound tends to change its properties smoothly and slowly (gradualness of change)''[2]. We will consider this in the following physical constraint.
Temporal differentiation of the amplitude envelope Ak(t) must be
represented by Rth-order differentiable polynomial
Ck,R(t) as follows:
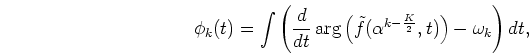
Applying Physical constraint 1 into Eq. (![]() ), a linear
differential equation is obtained as follows:
), a linear
differential equation is obtained as follows:
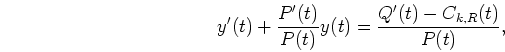 ,
,
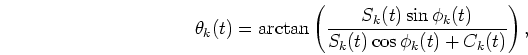 is called the ``unknown function.''
is called the ``unknown function.''
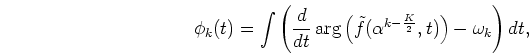
If Ck(t) is determined, then
![]() is uniquely
determined by the above equation.
Although it is possible to estimate the coefficients
is uniquely
determined by the above equation.
Although it is possible to estimate the coefficients
![]() by considering as an optimization problem,
we will assume, in order to reduce the computational costs that in
small segment
by considering as an optimization problem,
we will assume, in order to reduce the computational costs that in
small segment ![]() ,
Ck,R(t)=Ck,0.
As this point, Eq. (
,
Ck,R(t)=Ck,0.
As this point, Eq. (![]() ) is equivalent to
dAk(t)/dt=0, and amplitude envelope Ak(t) does not fluctuate
in small segment
) is equivalent to
dAk(t)/dt=0, and amplitude envelope Ak(t) does not fluctuate
in small segment ![]() .
.
Next, we will use regularity (ii) to segregate each small segment
![]() .
Regularity (ii) means that ``each physical parameter must retain
temporal proximity in the bound (t=Tr) between pre-segment
(
.
Regularity (ii) means that ``each physical parameter must retain
temporal proximity in the bound (t=Tr) between pre-segment
(
![]() )
and post-segment (
)
and post-segment (
![]() ).''
In order to apply this regularities to physical parameters, it is
considered in the following physical constraint.
).''
In order to apply this regularities to physical parameters, it is
considered in the following physical constraint.
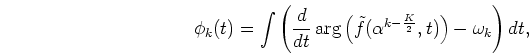
From Eqs. (![]() ), (
), (![]() ) and (
) and (![]() ),
amplitude envelopes Ak(t) and Bk(t), and input phase
),
amplitude envelopes Ak(t) and Bk(t), and input phase
![]() are functions of the unknown coefficient.
Therefore, by considering the above relationships, we can interpret
physical constraint 2 in order to determine Ck,0, which is
restricted within
are functions of the unknown coefficient.
Therefore, by considering the above relationships, we can interpret
physical constraint 2 in order to determine Ck,0, which is
restricted within
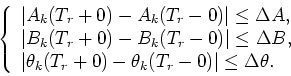 |
(22) |
Finally, we will apply regularity (iii). This regularity states that ``many changes take place in an acoustic event that affect all the components of the resulting sound in the same way and at the same time'' [2]. This regularity is considered the following physical constraint.
The amplitude envelope Bk(t) must be highly correlated with the
amplitude envelope
![]() obtained by the output of adjacent channel:
obtained by the output of adjacent channel:
| (23) |
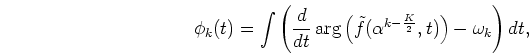
Since an amplitude envelope Bk(t) is a function of Ck,0 from
Eqs. (![]() ) and (
) and (![]() ), and let
), and let
![]() be
an amplitude envelope Bk(t) determined by any Ck,0.
In addition, a correlation between amplitude envelopes is defined by
be
an amplitude envelope Bk(t) determined by any Ck,0.
In addition, a correlation between amplitude envelopes is defined by
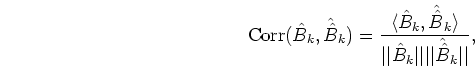 .
Let TB be an arbitrary past time, where integral region is
.
Let TB be an arbitrary past time, where integral region is
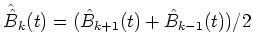 .
.