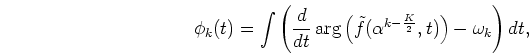Next: Simulations of segregation
Up: Calculation of physical parameters
Previous: Calculation of input phase
The theorem for segregation is obtained from previous lemma as follows.
Proof. Refer to Lemma 1 and 2. 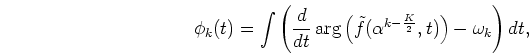
Segregation algorithm based on Theorem 1 is shown in Fig. ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) .
When the problem of segregating two acoustic sources is to be solved
using Theorem 1, signal duration which two signals exist in the same
time region must be known.
In Section 2, we assumed that when localized f1(t) is added to
f2(t), the signal duration can be detected using onset and offset
of f1(t).
By focusing on the temporal deviation of Sk(t) and
.
When the problem of segregating two acoustic sources is to be solved
using Theorem 1, signal duration which two signals exist in the same
time region must be known.
In Section 2, we assumed that when localized f1(t) is added to
f2(t), the signal duration can be detected using onset and offset
of f1(t).
By focusing on the temporal deviation of Sk(t) and  ,
onset and offset of f1(t) can be determined as follows:
,
onset and offset of f1(t) can be determined as follows:
- 1.
- Onset
 is determined by the nearest maximum point
of
is determined by the nearest maximum point
of
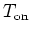 (within 25 ms) to the maximum point of
|dSk(t)/dt|.
(within 25 ms) to the maximum point of
|dSk(t)/dt|.
- 2.
- Offset
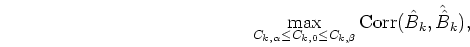 is determined by the nearest maximum point
of
is determined by the nearest maximum point
of
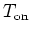 (within 25 ms) to the minimum point of
|dSk(t)/dt|.
(within 25 ms) to the minimum point of
|dSk(t)/dt|.
Therefore, the segregated duration is
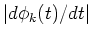 .
.



Next: Simulations of segregation
Up: Calculation of physical parameters
Previous: Calculation of input phase
Masashi Unoki
2000-10-26
![]() and
and
![]() ,
the input phase
,
the input phase
![]() can be determined using physical constraints 1-3 from
Eqs. (
can be determined using physical constraints 1-3 from
Eqs. (![]() ) and (
) and (![]() ).
Therefore, this problem can be solved using the amplitude envelope
Sk(t) and the output phase
).
Therefore, this problem can be solved using the amplitude envelope
Sk(t) and the output phase ![]() from Eqs. (
from Eqs. (![]() )-(
)-(![]() ).
).