


Next: Simulation 1
Up: A Method of Signal
Previous: Determination of Dk,0(t) using
We carried out three simulations on segregating two acoustic sources using noise-added signal f(t), to show that the proposed method can extract the desired signal f1(t) from the mixed signal f(t).
These simulations were composed as follows:
- 1.
- Extracting an AM complex tone from a noise-added AM complex tone.
- 2.
- Extracting one AM complex tone from mixed AM complex tones.
- 3.
- Extracting a speech signal (vowel) from a noisy speech.
In simulations 1 and 2 the fundamental frequency did not vary temporally, while in simulation 3 it did.
The purpose of simulation 1 was to examine the assumptions of the problem of segregating two acoustic sources;
the purpose of simulation 2 was to examine the case in which the concurrent signal component exists in the same frequency region; and
the purpose of simulation 3 was to examine whether the proposed method can be applied the problem of segregating a vowel from a noisy vowel.
We used two measures to evaluate the segregation performance of the proposed method.
One was the temporal average of the segregated error in terms of the instantaneous amplitude Ak(t).
The aim of using this measure was to evaluate the segregation in terms of the amplitude envelope where signal and noise exist in the same frequency region.
This measure is called ``Precision'', and is defined by
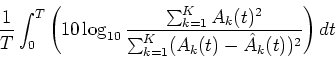 |
(34) |
where Ak(t) is the amplitude envelope of the original signal f1(t), and
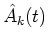 is the amplitude envelope of the segregated signal
is the amplitude envelope of the segregated signal
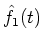 .
.
The other measure was the spectrum distortion.
The aim of using this measure was to evaluate the extraction of the desired signal
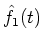 from noise-added signal f(t).
This measure is defined by
from noise-added signal f(t).
This measure is defined by
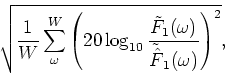 |
(35) |
where
 and
and
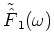 are the amplitude spectra of f1(t) and
are the amplitude spectra of f1(t) and
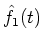 ,
respectively.
In the above equation, the frame length is 51.2 ms, the frame shift is 25.6 ms, W is the analyzable bandwidth of the filterbank (about 6 kHz), and the window function is Hamming.
,
respectively.
In the above equation, the frame length is 51.2 ms, the frame shift is 25.6 ms, W is the analyzable bandwidth of the filterbank (about 6 kHz), and the window function is Hamming.
Here, in the measure of precision, a higher value means high accuracy of segregation.
Conversely, in the measure of spectrum distortion, a lower value means high accuracy of segregation.
Next, in order to show the advantages of the constraints shown in Table II, we compare the following conditions for the three simulations:
- 1.
- Condition 1: Extract the harmonics using the Comb filter and predict Ak(t) using the Kalman filtering.
- 2.
- Condition 2: Extract the harmonics using the Comb filter.
- 3.
- Condition 3: Do nothing.
Here, condition 1 corresponds to constraint of gradualness of change (smoothness) being omitted;
condition 2 corresponds to constraints of gradualness of change (smoothness) and harmonicity being omitted;
and condition 3 corresponds to no constraints being applied at all.
The evaluated value of the noise reduction is the improvement in the two measures between using the proposed method and using condition 3.



Next: Simulation 1
Up: A Method of Signal
Previous: Determination of Dk,0(t) using
Masashi Unoki
2000-11-07
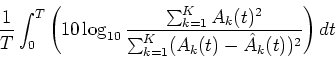
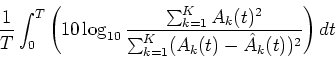
![]() from noise-added signal f(t).
This measure is defined by
from noise-added signal f(t).
This measure is defined by
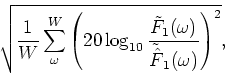
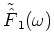 are the amplitude spectra of f1(t) and
are the amplitude spectra of f1(t) and