Separation block

The separation block determines A_k(t), B_k(t), $\theta_{1k}(t)$, and $\theta_{2k}(t)$ from S_k(t) and $\phi_k(t)$ using constraints (ii) and (iv) in the determined concurrent time-frequency region. In this paper, the improvement of the auditory sound segregation model is to reconsider the constraints on the continuity of $\theta_{1k}(t)$ as well as the constraints on the continuity of A_k(t) and F₀(t). Constraint (ii) is implemented such that C_k,R(t) and D_k,R(t) are linear (R=1) polynomials, in order to reduce the computational cost of estimating C_k,R(t) and D_k,R(t). In this assumption, A_k(t) and $\theta_{1k}(t)$, which can be allowed to undergo a temporal change in region, constrain the second-order polynomials ( $A_k(t)=\int C_{k,1}(t)dt+C_{k,0}'$ and $\theta_{1k}(t)=\int D_{k,1}(t)+D_{k,0}'$). Then, substituting dA_k(t)/dt=C_k,R(t) into Eq. (), we get the linear differential equation of the input phase difference $\theta_k(t)=\theta_{2k}(t)-\theta_{1k}(t)$. By solving this equation, a general solution is determined by

$$\theta_k(t)=\arctan\left(\frac{S_k(t)\sin(\phi_k(t)-\theta_{1k}(t))}{S_k(t)\cos(\phi_k(t)-\theta_{1k}(t))+C_k(t)}\right),$$ (6)

where $C_k(t)=-\int C_{k,R}(t)dt-C_{k,0}=-A_k(t)$ [7].

The signal flow of the separation block is shown in Fig. . In the segment T_h-T_h-1 which can be determined by E_0,R(t)=0, A_k(t), B_k(t), $\theta_{1k}(t)$, and $\theta_{2k}(t)$ are determined by the following steps. First, the estimated regions, $\hat{C}_{k,0}(t)-P_k(t) \leq C_{k,1}(t) \leq \hat{C}_{k,0}(t)+P_k(t)$ and $\hat{D}_{k,0}(t)-Q_k(t) \leq D_{k,1}(t) \leq \hat{D}_{k,0}(t)+Q_k(t)$, are determined by using the Kalman filter, where $\hat{C}_{k,0}(t)$ and $\hat{D}_{k,0}(t)$ are the estimated values and P_k(t) and Q_k(t) are the estimated errors. Next, the candidates of C_k,1(t) at any D_k,1(t) are selected by using the spline interpolation in the estimated error region. Then, $\hat{C}_{k,1}(t)$ is determined by using

$$\hat{C}_{k,1}=\mathop{\arg\max}_{\hat{C}_{k,0}-P_k\leq C_{k,1... ...\vert\hat{A}_k\vert\vert \vert\vert\hat{\hat{A}}_k\vert\vert},$$ (7)

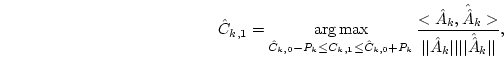where $\hat{A}_k(t)$ is obtained by the spline interpolation and $\hat{\hat{A}}_k(t)$ is determined in across-channel that satisfies constraint (iii). Finally, $\hat{D}_{k,1}(t)$ is determined by using

$$\hat{D}_{k,1}=\mathop{\arg\max}_{\hat{D}_{k,0}-Q_k\leq D_{k,1... ...\vert\hat{A}_k\vert\vert \vert\vert\hat{\hat{A}}_k\vert\vert}.$$ (8)

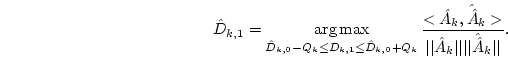Since $\theta_{1k}(t)$ and $\theta_k(t)$ are determined from $\hat{D}_{k,1}(t)$ and $\hat{C}_{k,1}(t)$, A_k(t), B_k(t), and $\theta_{2k}(t)$ can be determined from Eq. (), Eq. (), and $\theta_{2k}(t)=\theta_k(t)+\theta_{1k}(t)$, respectively.

  

Figure: Signal processing of a separation block.