| |
(1) |
Bregman has reported that the human auditory system uses four psychoacoustically heuristic regularities related to acoustic events to solve the problem of auditory scene analysis [1]. If an auditory sound segregation model was constructed using these regularities, it would be applicable not only to a preprocessor for robust speech recognition systems but also to various types of signal processing.
Some ASA-based segregation models already exist. There are two main types of models, based on either bottom-up [2] or top-down processes [3,4]. All these models use some of the four regularities, and the amplitude (or power) spectrum as the acoustic feature. Thus they cannot completely segregate the desired signal from noisy signal when the signal and noise exist in the same frequency region.
In contrast, we have discussed the need to use not only the amplitude spectrum but also the phase spectrum in order to completely extract the desired signal from a noisy signal, thus addressing the problem of segregating two acoustic sources [5].
This problem is defined as follows [5,7].
First, only the mixed signal f(t), where
f(t)=f1(t)+f2(t), can be observed.
Next, f(t) is decomposed into its frequency components by a filterbank (K channels).
The output of the k-th channel Xk(t) is represented by
| = | |||
 |
(4) | ||
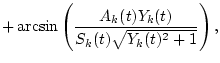 |
= | ||
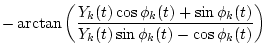 |
(5) |
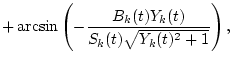 and
Zk(t)=Sk(t)2-Ak(t)2-Bk(t)2.
Hence, f1(t) and f2(t) can be reconstructed by using the determined pair of [Ak(t) and
and
Zk(t)=Sk(t)2-Ak(t)2-Bk(t)2.
Hence, f1(t) and f2(t) can be reconstructed by using the determined pair of [Ak(t) and
| Regularity (Bregman, 1993) | Constraint (Unoki and Akagi, 1999) | |
| (i) common onset/offset | synchronous of onset/offset |
|
| (ii) gradualness of change | piecewise-differentiable polynomial |
|
| approximation | dF0(t)/dt=E0,R(t) | |
| (smoothness) | (spline interpolation) |
|
|
|
||
| (iii) harmonicity | multiples of the fundamental frequency |
|
| (iv) changes occurring in | correlation between the instantaneous |
|
| the acoustic event | amplitudes |
To solve this problem, we have proposed a basic method of solving it using constraints related to the four regularities [5] and the improved method [6]. However, the former cannot deal with the variation of the fundamental frequency, although it can segregate the synthesized signal from the noise-added signal. Additionally, for the later, it is difficult to completely determine the phases, although it can be segregated vowel from noisy vowel precisely at certain amplitudes by constraining the continuity of the instantaneous amplitudes and fundamental frequencies.
This paper proposes a new sound segregation method to deal with real speech and noise precisely even in waveforms, by using constraints on the continuity of instantaneous phases as well as constraints on the continuity of instantaneous amplitudes and fundamental frequencies.