To show the advantages of the constraints in Table ![]() , we compared the performances of our method under 11-conditions as shown in Table
, we compared the performances of our method under 11-conditions as shown in Table ![]() .
In this simulation, we used two types of desired signal f1(t): simulation signal (a) and vowel /a/ of the male speaker (mau) in simulation signal (b); f2(t) was bandpassed pink-noise.
Conditions 1 - 3 denote sound segregation using three of the constraints.
Note that constraints (ii-b) and (iv) cannot be separately used because
Ck,1(t) and
Dk,1(t) are uniquely determined using these constraints.
Conditions 4 - 6 denote sound segregation using the two of the constraints.
Conditions 7 - 9 denote sound segregation using the only one of the constraints.
Note that utilizing constraint (ii-a) corresponds to estimating Ak(t) and
.
In this simulation, we used two types of desired signal f1(t): simulation signal (a) and vowel /a/ of the male speaker (mau) in simulation signal (b); f2(t) was bandpassed pink-noise.
Conditions 1 - 3 denote sound segregation using three of the constraints.
Note that constraints (ii-b) and (iv) cannot be separately used because
Ck,1(t) and
Dk,1(t) are uniquely determined using these constraints.
Conditions 4 - 6 denote sound segregation using the two of the constraints.
Conditions 7 - 9 denote sound segregation using the only one of the constraints.
Note that utilizing constraint (ii-a) corresponds to estimating Ak(t) and
![]() using the Kalman filter for any channels.
Condition 10 denotes sound segregation without all the constraints.
using the Kalman filter for any channels.
Condition 10 denotes sound segregation without all the constraints.
Segregation accuracy in this simulation for AM-FM complex tones is shown in Fig. ![]() .
Segregation accuracy in this simulation for vowel /a/ is shown in Fig.
.
Segregation accuracy in this simulation for vowel /a/ is shown in Fig. ![]() .
In these figures, segregation accuracy values above the dashed line show the improved accuracy, that is, noise reduction.
The results show that segregation accuracy achieved by the proposed model was the best among the constraints.
Moreover, comparisons between four groups (conditions 0-1-3-4-6-7, 0-1-2-3-4-5-9, 0-1-2-5-6-8, and 0-2-3) show that the absence of some constraints reduces the accuracy.
These groups were selected by focusing on only one constraint in Table
.
In these figures, segregation accuracy values above the dashed line show the improved accuracy, that is, noise reduction.
The results show that segregation accuracy achieved by the proposed model was the best among the constraints.
Moreover, comparisons between four groups (conditions 0-1-3-4-6-7, 0-1-2-3-4-5-9, 0-1-2-5-6-8, and 0-2-3) show that the absence of some constraints reduces the accuracy.
These groups were selected by focusing on only one constraint in Table ![]() and by omitting some of the constraints in turn.
Hence, all the constraints related to the four regularities are useful for segregating the desired vowel from a noisy vowel.
and by omitting some of the constraints in turn.
Hence, all the constraints related to the four regularities are useful for segregating the desired vowel from a noisy vowel.
An example of segregation in case of Fig. ![]() (c) is shown in Fig.
(c) is shown in Fig. ![]() .
An example of segregation in case of Fig.
.
An example of segregation in case of Fig. ![]() (c) is shown in Fig.
(c) is shown in Fig. ![]() .
.
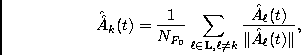 |