


Next: Appendix B: Candidate selection Ck,1(t) Dk,1(t)
Up: Bibliography
Previous: Bibliography
Table:
Definitions of symbols for the Kalman filtering
| Symbol |
Estimation of
Ck,0(t) |
Estimation of
Dk,0(t) |
Observed signal
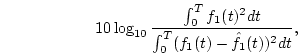 |
Xk(tm) |
 |
State variable
 |
Ck(tm) |
 |
Observed noise
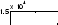 |
X2,k(tm) |
X2,k(tm)/Sk(tm) |
System noise
 |
wm |
wm |
State transition matrix
 |
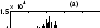 |
 |
Observation matrix
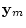 |
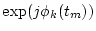 |
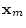 |
Driving matrix
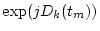 |
1 |
1 |
Initial value
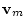 |
0 |
1 |
Initial value
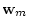 |
Sk(t0) |
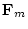 |
In this paper, we consider how to estimate Ck,0 and Dk,0 from the observed component Xk(t) using the Kalman filter.
The estimation duration is
[Th-1-Th].
It is then decomposed into discrete time
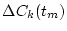 ,
,
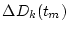 , where the sampling period is
, where the sampling period is
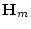 and fs is the sampling frequency.
First, let Ck(t) and Dk(t) be
and fs is the sampling frequency.
First, let Ck(t) and Dk(t) be
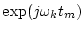 and
and
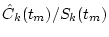 , respectively.
Here, let the temporal variations of Ck(t) and Dk(t) at discrete time tm be
, respectively.
Here, let the temporal variations of Ck(t) and Dk(t) at discrete time tm be
| Ck(tm+1) |
= |
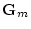 |
(37) |
 |
= |
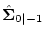 |
(38) |
| Dk(tm+1) |
= |
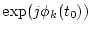 |
(39) |
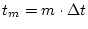 |
= |
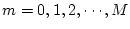 |
(40) |
where
t0=Th-1 and tM=Th.
It is assumed that the variation error is represented by white noise with mean 0 and variance
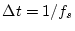 .
.
Next, for the system of the Kalman filtering problem:
in order to estimate
Ck,0(t),
we apply Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) to Eq. (
) to Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and apply Eq. (
) and apply Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) to Eq. (
) to Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ).
Using the same steps as for the system of the Kalman filtering problem, in order to estimate
Dk,0(t), we apply Eq. (
).
Using the same steps as for the system of the Kalman filtering problem, in order to estimate
Dk,0(t), we apply Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) to Eq. (
) to Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and apply the normalized Eq. (
) and apply the normalized Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) to Eq. (
) to Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ).
The parameters in Eqs. (
).
The parameters in Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) are shown in Table
) are shown in Table ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) .
.
In these systems, the mean and variance of the terms,
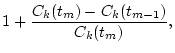 ,
,
 , and
, and
 , are known.
And
, are known.
And
 ,
,
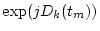 ,
,
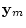 , and
, and
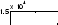 are known matrices.
The Kalman filtering problem is to determine the minimum variance requirement
are known matrices.
The Kalman filtering problem is to determine the minimum variance requirement
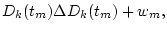 from the observed
from the observed
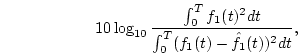 ,
,
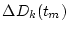 as follows.
as follows.
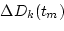 |
(43) |
It is calculated by sequentially solving the following equations:
- 1.
- Filtering equation
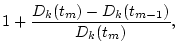 |
|
|
(44) |
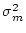 |
|
|
(45) |
- 2.
- Kalman gain
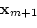 |
(46) |
- 3.
- Covariance equation for the estimated-error
- 4.
- Initial state
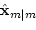 |
(49) |
The symbols
 and
and
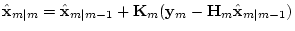 are the mean and variance of a random variable, respectively.
are the mean and variance of a random variable, respectively.
Finally, performing the Kalman filtering according to Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ), we obtain the minimal-variance estimated value
), we obtain the minimal-variance estimated value
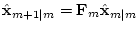 and the covariance matrix
and the covariance matrix
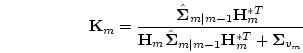 at discrete time tm.
As a result, the estimated
at discrete time tm.
As a result, the estimated
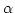 and
and
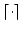 , and the estimated errors Pk(t) and Qk(t) are determined by
, and the estimated errors Pk(t) and Qk(t) are determined by
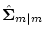 and
and
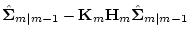 ,
,
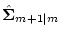 , and
, and
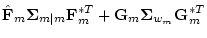 , respectively.
, respectively.



Next: Appendix B: Candidate selection Ck,1(t) Dk,1(t)
Up: Bibliography
Previous: Bibliography
Masashi Unoki
2000-10-26
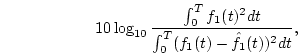
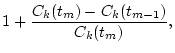 ,
,
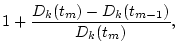
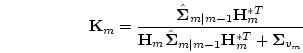 at discrete time tm.
As a result, the estimated
at discrete time tm.
As a result, the estimated