 |
(19) |
The problem of segregating the desired signal from a noisy signal is an important issue not only in robust speech recognition systems but also in various types of signal processing. It has been investigated by many researchers, who have proposed many methods. For example, in the investigation of robust speech recognition [Furui and Sondhi1991], there are noise reduction or suppression [Boll1979] and speech enhancement methods [Junqua and Haton1996]. In the investigation of signal processing, there is signal estimation using a linear system [Papoulis1977] and signal estimation based on a stochastic process for signal and noise [Papoulis1991]. One recent proposal is Blind Separation [Shamsunder and Giannakis1997] which estimates the inverse-translation-operator (input-output translation function) by using the observed signal in order to estimate the original input.
However, in practice, it is difficult to segregate each original signal from a mixed signal, because this problem is an ill-posed inverse problem and the signals exist in a concurrent time-frequency region. Therefore, it is difficult to solve this problem without using constraints on acoustic sources and the real environment.
On the other hand, the human auditory system can easily segregate the desired signal in a noisy environment that simultaneously contains speech, noise, and reflections. Recently, this ability of the auditory system has been regarded as a function of an active scene analysis system. Called "Auditory Scene Analysis (ASA)", it has become widely known as a result of Bregman's book [Bregman1990]. Bregman has reported that the human auditory system uses four psychoacoustically heuristic regularities related to acoustic events, to solve the problem of Auditory Scene Analysis. These regularities are
Some ASA-based investigations have shown that it is possible to solve the segregation problem by applying constraints to sounds and the environment. These approaches are called "Computational Auditory Scene Analysis (CASA)". Some CASA-based sound segregation models already exist. There are two main types of models, based on either bottom-up or top-down processes. Typical bottom-up models include an auditory sound segregation model based on acoustic events [Cooke1993,Brown1992], a concurrent harmonic sounds segregation model based on the fundamental frequency [de Cheveigne1993,de Cheveigne1997], and a sound source separation system with the ability of automatic tone modeling [Kashino and Tanaka1993]. Typical top-down models include a segregation model based on psychoacoustic grouping rules [Ellis1994,Ellis1996] and a computational model of sound segregation agents [Nakatani et al.1994,Nakatani et al.1995a,Nakatani et al.1995b]. All these models use some of the four regularities, and the amplitude (or power) spectrum as the acoustic feature. Thus they cannot completely extract the desired signal from a noisy signal when the signal and noise exist in the same frequency region.
In contrast, we have been tackling the problem of segregating two acoustic sources as a fundamental problem, and considering that it can be uniquely solved using not only amplitude but also phase information and using mathematical constraints related to the four psychoacoustically heuristic regularities [Unoki and Akagi1997a,Unoki and Akagi1999].
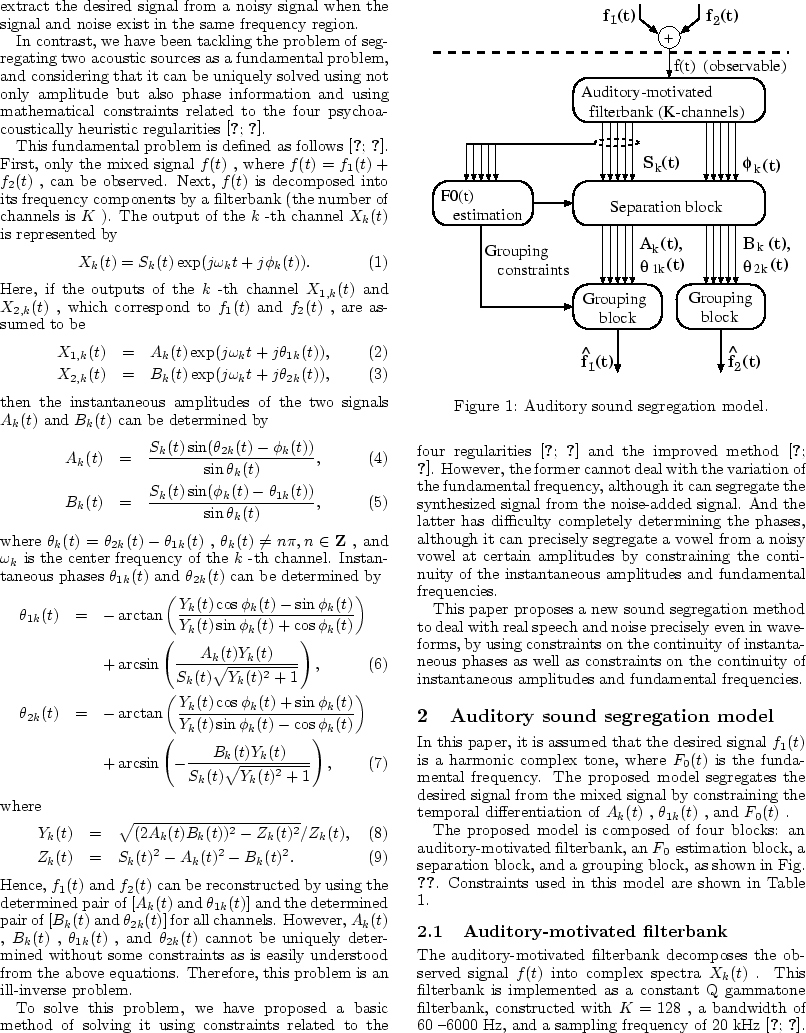
This fundamental problem is defined as follows [Unoki and Akagi1997a,Unoki and Akagi1999].
First, only the mixed signal f(t), where
f(t)=f1(t)+f2(t), can be observed.
Next, f(t) is decomposed into its frequency components by a filterbank (the number of channels is K).
The output of the k-th channel Xk(t) is represented by
| X1,k(t) | = | 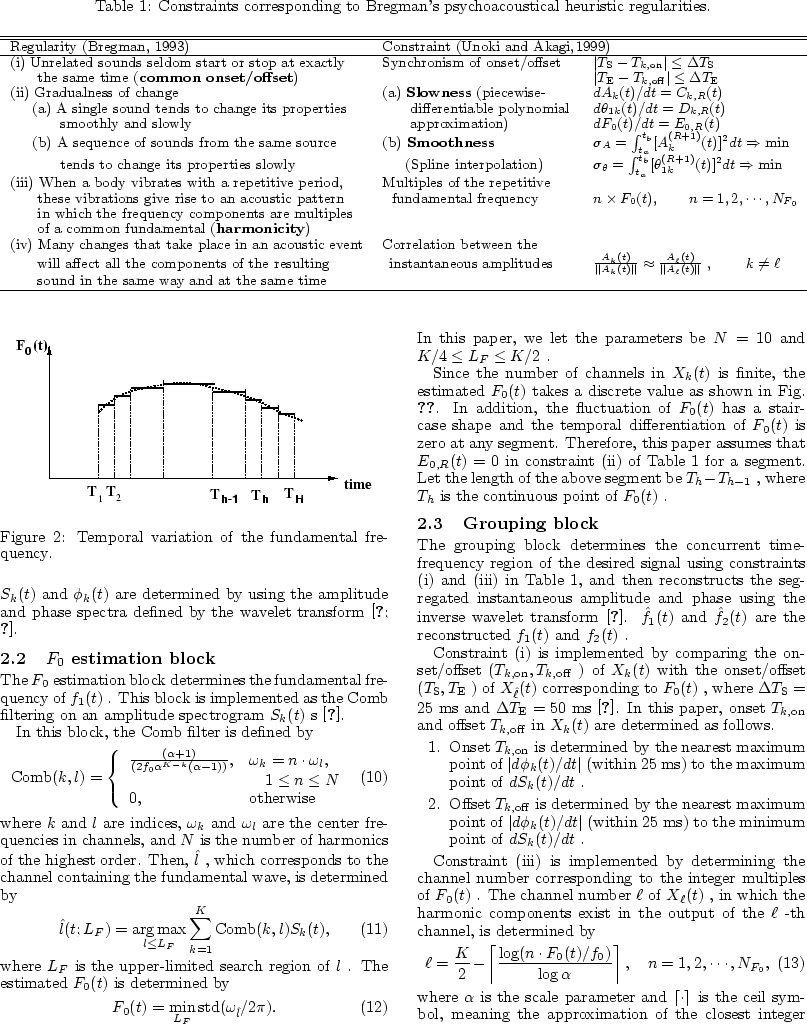 |
(20) |
| X2,k(t) | = |  |
(21) |
 ,
,
 , and
, and 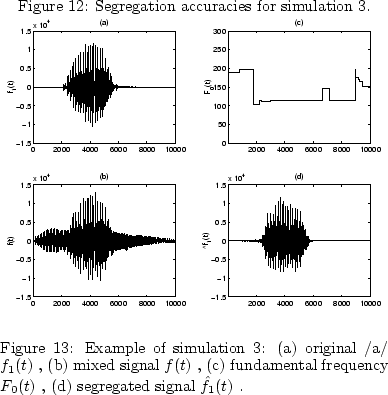 is the center frequency of the k-th channel.
Instantaneous phases
is the center frequency of the k-th channel.
Instantaneous phases
| = | |||
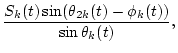 |
(24) | ||
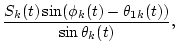 |
= | ||
| (25) |
| Yk(t) | = | (26) | |
| Zk(t) | = | Sk(t)2-Ak(t)2-Bk(t)2. | (27) |
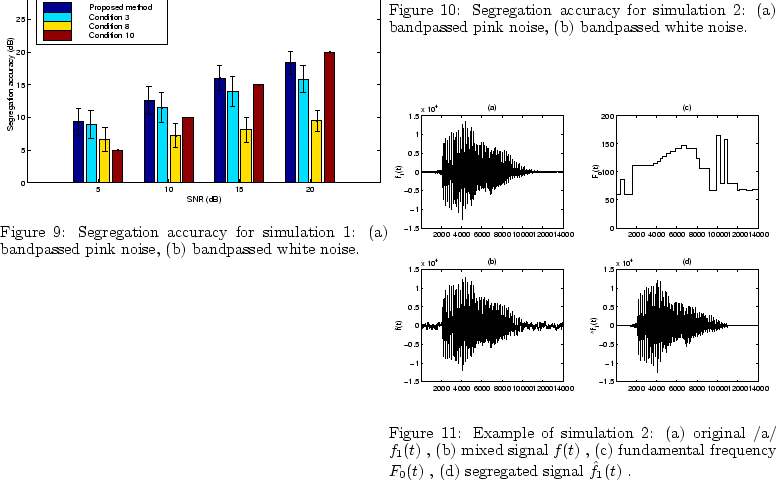
To solve this problem, we have proposed a basic method of solving it using constraints related to the four regularities [Unoki and Akagi1997b,Unoki and Akagi1997c] and the improved method [Unoki and Akagi1998,Unoki and Akagi1999]. However, the former cannot deal with the variation of the fundamental frequency, although it can segregate the synthesized signal from the noise-added signal. And the latter has difficulty completely determining the phases, although it can precisely segregate a vowel from a noisy vowel at certain amplitudes by constraining the continuity of the instantaneous amplitudes and fundamental frequencies.
This paper proposes a new sound segregation method to deal with real speech and noise precisely even in waveforms, by using constraints on the continuity of instantaneous phases as well as constraints on the continuity of instantaneous amplitudes and fundamental frequencies.