Constraint of envelopes with periodicity

  

Figure: Original signal /a/ (top) and its instantaneous amplitudes, A_k(t)s (bottom).

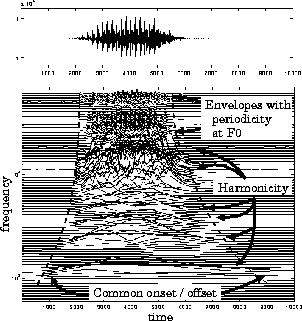
Fig. 4 shows an original signal /a/ and its instantaneous amplitudes, A_k(t)s. Channel envelopes with periodicity at the fundamental frequency F₀(t) exist at higher frequencies. This is caused by using constant Q filterbank.

In our previous model, the constraint of common onset and offset often failed to extract channel envelopes with the original added white noise, but the constraint could extract channel envelopes with the original added pink noise. This is because the power of noise components at a higher frequency disturbed the detection of the onset and offset of the desired signal using constraint (i).

We reconsider constraint (iv) to solve this problem. We divide constraint (iv) into two temporal modulations: slow modulation and fast modulation. Then, we regard slow temporal modulation as common fluctuations of A_k(t) and regard the fast temporal modulation as channel envelopes with periodicity at the fundamental frequency.

In order to detect channel envelopes with periodicity at F₀(t), we implement a detection of the difference between F₀(t) and $\hat{F}_0(t)$ as the fast modulation, where F₀(t) is determined by the F₀ estimation block and $\hat{F}_0(t)$ is estimated by using the autocorrelation between S_k(t) for any t as follows.

$$A_{\rm {corr},k}(t,\tau) \frac{1}{T}\int_t^{t+T} S_k(x)S_k(x+\tau)dx,$$ = (13)

$$\hat{T}_0(t) \displaystyle{\mathop{\arg\max}_{\tau_{\min} \leq \tau \leq \tau_{\max}}} A_{\rm {corr},k}(t,\tau),$$ = (14)

$$\hat{F}_0(t) 1/\hat{T}_0(t),$$ = (15)

where $\tau_{\min}=1/400$, $\tau_{\max}=1/60$, T=1/60, and $\tau$ is lag length. The above common value, 60, means the lowest frequency of the filterbank. In this paper, $\Delta F_0$ of constraint (iv-b) in Table 1 is 10 Hz.