Auditory sound segregation model

 

 

Table: Constraints corresponding to Bregman's psychoacoustical heuristic regularities.

Regularity (Bregman, 1993)	Constraint (Unoki and Akagi,	1999)
(i) Unrelated sounds seldom start or stop at exactly	Synchronism of onset/offset	$\vert T_{\rm {S}}-T_{k,\rm {on}}\vert \leq \Delta T_{\rm {S}}$
the same time ( common onset/offset)		$\vert T_{\rm {E}}-T_{k,\rm {off}}\vert \leq \Delta T_{\rm {E}}$
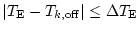(ii) Gradualness of change	(a) Slowness (piecewise-	dAk(t)/dt=Ck,R(t)
(a) A single sound tends to smoothly and slowly	differentiable polynomial	$d\theta_{1k}(t)/dt=D_{k,R}(t)$
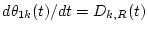change its properties	approximation)	dF0(t)/dt=E0,R(t)
(b) A sequence of sounds from the same source	(b) Smoothness	$\sigma_A=\int_{t_a}^{t_b} [A_k^{(R+1)}(t)]^2dt \Rightarrow \min$
tends to slowly change its properties	(Spline interpolation)	$\sigma_\theta=\int_{t_a}^{t_b} [\theta_{1k}^{(R+1)}(t)]^2dt \Rightarrow \min$
		$\sigma_{A_k}=\sum_k [(\log A_k(t))^{(R+1)}]^2$
		$\Rightarrow \min$ (new)
(iii) When a body vibrates with a repetitive period,	Multiples of the repetitive
these vibrations give rise to an acoustic pattern	fundamental frequency	$n\times F_0(t), \qquad n=1,2,\cdots, N_{F_0}$
in which the frequency components are multiples		$\ell=\frac{K}{2}-\left\lceil \frac{\log(n\cdot F_0(t)/f_0)}{\log\alpha} \right\rceil$
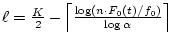of a common fundamental ( harmonicity)
(iv) Many changes that take place in an acoustic	(a) Slow modulation
event will affect all components of the result-	Correlation between the	$\frac{A_k(t)}{\Vert A_k(t)\Vert} \approx \frac{A_{\ell}(t)}{\Vert A_\ell(t)\Vert}$, $\qquad k\not=\ell$
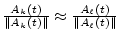ing sound in the same way and at the	instantaneous amplitudes
same time	(b) Fast modulation
	Channel envelopes with	$\vert F_0(t)-\hat{F}_0(t)\vert\leq \Delta F_0$ (new)
	periodicity at the F0(t)

  

Figure: Auditory sound segregation model.

In this paper, the desired signal f₁(t) is assumed to be a harmonic complex tone, where F₀(t) is the fundamental frequency. The proposed model segregates the desired signal from the mixed signal by constraining the temporal differentiation of A_k(t), $\theta_{1k}(t)$, and F₀(t).

The proposed model is composed of four blocks: an auditory-motivated filterbank, an F₀ estimation block, a separation block, and a grouping block, as shown in Fig. 1. Constraints used in this model are shown in Table 1.