| f1(t) | = | (26) | |
| g1(t) | = | (27) | |
| f21(t) | = | 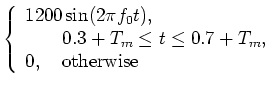 |
|
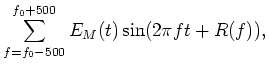 |
(28) | ||
| f22(t) | = | ||
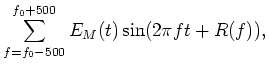 |
(29) |
For experimental stimuli, we will assume f1(t) is a sinusoidal signal
and f2(t) are two types of noise where f21(t) is an AM
bandpassed noise and f22(t) is a bandpassed random noise, as follows:
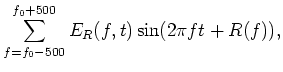 is a bandpass filter with a center
frequency f0 and a bandwidth of 23 Hz (as shown in
Fig.
is a bandpass filter with a center
frequency f0 and a bandwidth of 23 Hz (as shown in
Fig.
The two types of mixed signals are
fM(t)=f1(t)+f21(t) when
f2(t)=f21(t) and
fR(t)=f1(t)+f22(t) when
f2(t)=f22(t).
When a human hears these mixed signals, he can hear the sinusoidal
signal from fM(t) caused by CMR; however cannot hear the sinusoidal
signal from fR(t) caused by Masking.
These mixed signals are shown in Fig. ![]() .
.
In this simulation, segregation is done using 10 mixed signals which
are made by varying the onset of f1(t),
![]() in Eq.
(
in Eq.
(![]() ).
).