First, simulation of segregation are conducted using 10 mixed signals
fM(t).
fM(t) is decomposed by a wavelet filterbank, and is then applied
to the segregation algorithm as shown in Fig. ![]() .
Sk(t) and
.
Sk(t) and ![]() are determined as shown in Fig.
are determined as shown in Fig. ![]() .
Onset time and offset time of f1(t),
.
Onset time and offset time of f1(t),
![]() and
and
![]() ,
are determined as shown in Fig.
,
are determined as shown in Fig. ![]() .
The results of simulation for a sinusoidal signal (m=0) as shown in Fig.
.
The results of simulation for a sinusoidal signal (m=0) as shown in Fig.
![]() are shown in Fig.
are shown in Fig. ![]() .
From this figure, it can be seen that the proposed method can extract a
sinusoidal signal from mixed signal.
.
From this figure, it can be seen that the proposed method can extract a
sinusoidal signal from mixed signal.
Similarly, simulations of segregation are carried out using 10 mixed signals fR(t). The proposed model extracts so little of f1(t) that f2(t)becomes approximately the same as f(t).
When the extracted signal corresponds to 10 mixed signals, the mean
value of SNR in the time region is calculated as
| (30) |
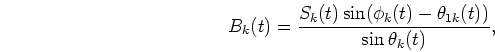 is
12.9 dB (standard deviation 2.58) and the SNR of
is
12.9 dB (standard deviation 2.58) and the SNR of
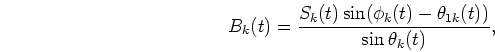 is 1.6 dB
(standard deviation 1.58) and the SNR of
is 1.6 dB
(standard deviation 1.58) and the SNR of
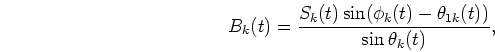 is the enhanced signal, the SNR of
is the enhanced signal, the SNR of
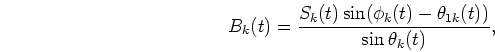 is
only 8.1 dB.
From these results, it can be stated that the proposed method is
superior in improving SNR in comparison with method using BPF.
In the case of fM(t), the proposed method can not only extract a
sinusoidal signal more accurately than fR(t) but can also a
bandpassed noise.
While engineering application call for a method of segregating all
signals from noisy signals, the proposed method successfully extracts
signals by taking advantage of the constraints of ASA (c. f.
fM(t)).
Note that the above results show of CMR which is as the human auditory
phenomenon.
To examine this similarity, we will carry out a simulation of CMR in
next section by setting the model parameters to the human auditory
properties.
is
only 8.1 dB.
From these results, it can be stated that the proposed method is
superior in improving SNR in comparison with method using BPF.
In the case of fM(t), the proposed method can not only extract a
sinusoidal signal more accurately than fR(t) but can also a
bandpassed noise.
While engineering application call for a method of segregating all
signals from noisy signals, the proposed method successfully extracts
signals by taking advantage of the constraints of ASA (c. f.
fM(t)).
Note that the above results show of CMR which is as the human auditory
phenomenon.
To examine this similarity, we will carry out a simulation of CMR in
next section by setting the model parameters to the human auditory
properties.