


Next: Calculation of the four
Up: Auditory segregation model
Previous: Formulation of the problem
Firstly, we describe the wavelet transform and the inverse wavelet transform to design an auditory filterbank.
If
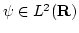 satisfies the ``admissibility'' condition:
satisfies the ``admissibility'' condition:
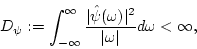 |
(9) |
where
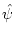 is Fourier transform of
is Fourier transform of 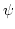 ,
then
,
then 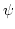 is called a ``basic wavelet''.
Relative to every basic wavelet
is called a ``basic wavelet''.
Relative to every basic wavelet 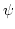 ,
the integral wavelet transform on
,
the integral wavelet transform on
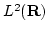 is defined by
is defined by
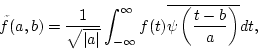 |
(10) |
where a is the ``scale parameter'', b is the ``shift parameter'', and
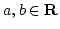 with
with 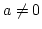 .
In addition, under this additional assumption, it follows that
.
In addition, under this additional assumption, it follows that
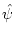 is a continuous function, so that finiteness of
is a continuous function, so that finiteness of 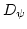 in Eq. (
in Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) implies
) implies
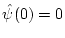 ,
or equivalently,
,
or equivalently,
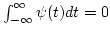 .
.
If 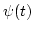 is a basic wavelet, then the inverse wavelet transform exist for all t as follows:
is a basic wavelet, then the inverse wavelet transform exist for all t as follows:
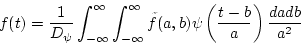 |
(11) |
Moreover, if we let 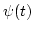 be a complex basic wavelet, then the integral wavelet transform can be represented by
be a complex basic wavelet, then the integral wavelet transform can be represented by
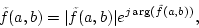 |
(12) |
where
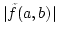 is the amplitude spectrum and
is the amplitude spectrum and
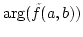 is the phase spectrum.
is the phase spectrum.
Secondly, to construct an auditory filterbank, we use the gammatone filter as an analyzing wavelet.
The gammatone filter is an auditory filter designed by Patterson[Patterson et al.1994], and simulates the response of the basilar membrane.
The impulse response of the gammatone filter is given by
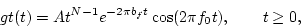 |
(13) |
where
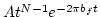 is the amplitude term represented by Gamma distribution and f0 is the center frequency.
In addition, amplitude characteristics of the gammatone filter are represented approximately by
is the amplitude term represented by Gamma distribution and f0 is the center frequency.
In addition, amplitude characteristics of the gammatone filter are represented approximately by
![\begin{displaymath}GT(f)\approx \left[1+\frac{j(f-f_0)}{b_f}\right]^{-N},\qquad 0 < f < \infty,
\end{displaymath}](img36.gif) |
(14) |
where GT(f) is the Fourier transform of gt(t).
The characteristics of the gammatone filter are shown in Fig. ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) .
To determine phase information, we extend the impulse response of the gammatone filter, which is a basic wavelet.
This basic wavelet is represented by
.
To determine phase information, we extend the impulse response of the gammatone filter, which is a basic wavelet.
This basic wavelet is represented by
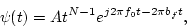 |
(15) |
using the Hilbert transform.
This analyzing wavelet satisfies the admissibility condition approximately, because
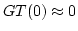 .
.
Figure:
Impulse response and amplitude characteristics of the gammatone filter (f0=600 Hz, N=4, bf=22.99).
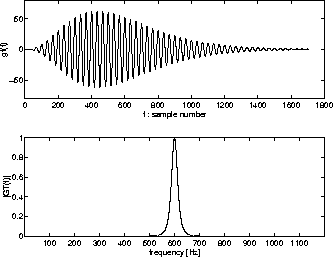 |
Figure:
Frequency characteristics of the wavelet filterbank.
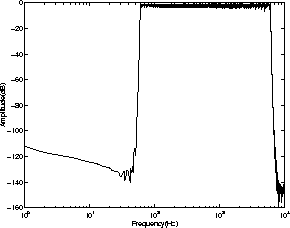 |
Finally, an auditory filterbank is designed with a center frequency f0 of 600 Hz, a bandpassed region from 60 Hz to 6000 Hz, and a number of filters K of 128.
This auditory filterbank is implemented on computer, using a discrete wavelet transform with the following conditions:
sampling frequency fs=20 kHz, the scale parameter
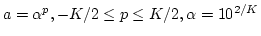 ,
and the shift parameter b=q/fs, where
,
and the shift parameter b=q/fs, where
 .
Frequency characteristics of the wavelet filterbank are shown in Fig.
.
Frequency characteristics of the wavelet filterbank are shown in Fig. ![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) .
.



Next: Calculation of the four
Up: Auditory segregation model
Previous: Formulation of the problem
Masashi Unoki
2000-10-26
![]() satisfies the ``admissibility'' condition:
satisfies the ``admissibility'' condition:
![]() is a basic wavelet, then the inverse wavelet transform exist for all t as follows:
is a basic wavelet, then the inverse wavelet transform exist for all t as follows:

![]() ,
and the shift parameter b=q/fs, where
,
and the shift parameter b=q/fs, where
![]() .
Frequency characteristics of the wavelet filterbank are shown in Fig.
.
Frequency characteristics of the wavelet filterbank are shown in Fig. ![]() .
.