


Next: Simulations
Up: A Method of Signal
Previous: Conclusion
-
decompose f(t) into its frequency components using the
wavelet filterbank (wavelet transform) as Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
for k:=1 to K do
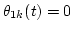 and
and 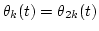 ;
;
determine Sk(t) and 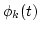 from Lemma 1;
from Lemma 1;
determine onset 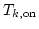 and offset
and offset 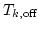 ;
;
the segregated duration is 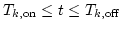 ;
;
if Physical constraint 4 or 5 is satisfied 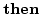
estimate Ck(t) using the Kalman filter;
determine the interpolated duration;
let I be the number of the interpolated samples;
for i=1 to I do
determine the candidates for Ck(t), which
interpolated by the spline function within
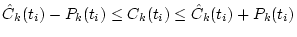 ;
;
determine 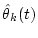 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine 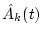 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine 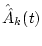 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine 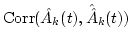 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
end
determine Ck(t) when 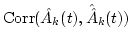
becomes a maximum within the estimated
-error;
determine  from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
else
set Ak(t)=0, Bk(t)=Sk(t) and 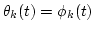 ;
;
end
determine Ak(t) and Bk(t) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine each frequency components of f1(t)
and f2(t) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
end
reconstruct 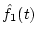 and
and 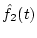 using the wavelet filterbank
using the wavelet filterbank
(inverse wavelet transform) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
99
decompose f(t) into its frequency components using the
wavelet filterbank (wavelet transform) as Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
for k:=1 to K do
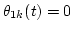 and
and 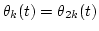 ;
;
determine Sk(t) and 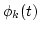 from Lemma 1;
from Lemma 1;
determine onset 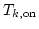 and offset
and offset 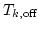 ;
;
the segregated duration is 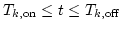 ;
;
if Physical constraint 4 or 5 is satisfied 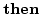
estimate Ck(t) using the Kalman filter;
determine the interpolated duration;
let I be the number of the interpolated samples;
for i=1 to I do
determine the candidates for Ck(t), which
interpolated by the spline function within
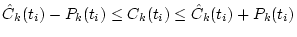 ;
;
determine 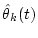 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine 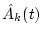 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine 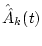 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine 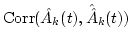 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
end
determine Ck(t) when 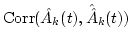
becomes a maximum within the estimated
-error;
determine  from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
else
set Ak(t)=0, Bk(t)=Sk(t) and 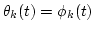 ;
;
end
determine Ak(t) and Bk(t) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
determine each frequency components of f1(t)
and f2(t) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);
end
reconstruct 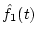 and
and 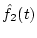 using the wavelet filterbank
using the wavelet filterbank
(inverse wavelet transform) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) );
);



Next: Simulations
Up: A Method of Signal
Previous: Conclusion
Masashi Unoki
2000-10-26
);
and
;
from Lemma 1;
and offset
;
;
;
from Eq. (
);
from Eq. (
);
from Eq. (
);
from Eq. (
);
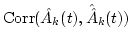
from Eq. (
);
;
) and (
);
) and (
);
and
using the wavelet filterbank
) and (
);