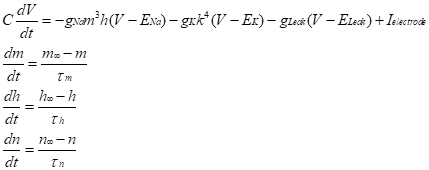Background, advanced: 膜興奮性や興奮伝導に関する生理学的基礎について。

１．細胞膜とイオン環境

細胞は細胞膜によって外界から明瞭に区別された構造で、生体を構成する基本単位である。電子素子における素過程が電子の動きであるのに対し、生体電気信号の素過程は膜を介したイオンの流出入である。

1.1　細胞膜の特徴

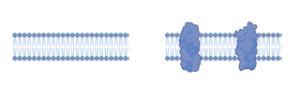
リン脂質と膜タンパク質が主成分である。リン脂質とは具体的に、ホスファチジルコリン、スフィンゴミエリン、ホスファチジルエタノールアミン、ホスファチジルセリンなどの両親媒性分子である。これらの分子は溶液中で2層の疎水部どうしが会合し親水性部が水相に接した厚さ4ナノメートル程度の脂質二重膜とよばれる安定構造をとる。膜タンパク質は脂質二重膜中を浮遊、あるいは、細胞膜直下の骨格構造にアンカーされている。純粋なリン脂質の二重膜はイオン透過性がほとんどなく、抵抗値は10^６～10^９Ω・cm² と高い値を示す。これに対して膜タンパク質を含む生体膜は10²～10⁵ Ω・cm²程度である。膜容量はリン脂質二重膜、細胞膜のどちらもおよそ1 mF/cm²程度である（文献１）。

（図1）リン脂質2重膜（左）と細胞膜（右）の模式図

１.2　静止膜電位

外径1 ~ 1.5 mm、壁厚0.2～0.3 mm程度の硝子管の一部を加熱・延伸し、内部を3 M塩化カリウム水溶液などの電解質を満たすと、先端径1 mm以下でありながら機械強度のあるガラス管微小電極ができる。マイクロマニュピレータを用いて電極を細胞に刺入し、高入力インピーダンスの増幅器で細胞外に配置した参照電極に対する電位を計測すると多くの場合 -30 ～ -80 mVの負の値を示し、これを細胞の静止膜電位と呼ぶ。細胞内外を媒質の抵抗値は細胞膜のそれに比べると顕著に低く、観察された電位差のほとんど(・・・・)は細胞膜をよぎる電位差に由来する。

1.3　静止膜電位の生成原理

細胞内では食物由来のエネルギーを用いてATP（アデノシン三リン酸）が合成されている。ATPの加水分解エネルギー（DG^o’ = 7.3 kcal/mol）は、様々な化学反応を促進することに利用されるが、その中には細胞内外のイオン環境を非対称に維持することが含まれている。Na⁺/K⁺ ATPアーゼという膜タンパク質は、

3Na⁺_[in] + 2K⁺_[out] + ATP + H₂O  ⇔　3Na⁺_[out] + 2K⁺_[in] + ADP + Pi

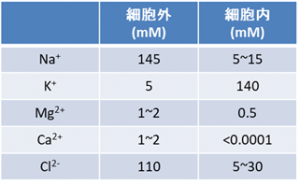
という反応を触媒する。ここで、[in], [out] はそれぞれ細胞内、細胞外にあるイオンであることを表す。こうした仕組みの結果、カリウムイオン濃度は細胞内で高く、細胞外では低くなり、ナトリウムイオンは逆に細胞内が薄いという環境が維持される（図２）。尚、このNa⁺/K⁺-ATPaseであるが、通常の細胞で合成されるATPの3割、神経細胞に至っては7割を消費していると見積もられている（文献２）。

（図２）一般的な細胞におけるイオン環境

 そして一般的に細胞膜はもう一つ重要な性質としてカリウムイオンに対する透過性を持っている。この透過性は背景漏洩カリウム電流とも呼ばれ、K2Pチャネルと呼ばれる膜蛋白質などが関与すると考えられている。一方で、静止状態におけるナトリウムイオンの透過性は通常は非常に低い。

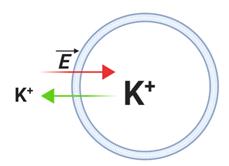
カリウムイオンに関して考えると、細胞内外で濃度差があり、しかも細胞膜はイオン透過性を持つのであれば、濃度が均一になる方向、即ち、細胞の内から外にイオンが拡散する効果が生じる（図３；緑矢印）。このようなカリウムイオンの移動が起きると、細胞内の正電荷が流出することにより細胞内は外に比べて負の電位になる。つまり電位勾配はカリウムイオンを細胞内側に戻す効果をもつ（図３；赤矢印）。この拡散の効果と、それと逆向きの静電的な効果が拮抗するところで平衡状態となる。

図３　カリウムイオン平衡と静止膜電位

 この平衡の定量的な記述として、ポテンシャル存在下での拡散による流速を記述するネルンスト・プランクの式

において、平衡状態（J＝０）として積分することで次のネルンストの式が得られる。

ここでJ：流速、D：拡散係数、c：濃度、R：気体定数、F：ファラデー定数、T：絶対温度、z：価数、φ：ポテンシャルである。ネルンストの式は、平衡に達したときの電位差Eと、細胞内外の濃度、C_in, C_out を関連付ける。Eは平衡電位やネルンスト電位と呼ばれる。カリウムイオン濃度がC_out = 4 mM; C_in = 140 mM, 温度が37度の時の平衡電位はE_K  = -89 mVとなる。多くの細胞種においてカリウムイオンに対する透過性が高いので、静止膜電位はカリウムイオンの平衡電位に近い値になる。これが静止膜電位の発生原理である。

一方でナトリウムイオンの平衡電位をC_out =145 mM; C_in = 10 mMとして計算すれば E_Na = +67 mVとなる。静止膜電位にある細胞はナトリウムイオンの観点からみると平衡から大きくずれている。後述するように、この「ずれ」は電気信号の発生において重要な役割を果たす。

 1.4　分極と脱分極

このようにして静止状態において細胞内は外に対して負電位になっている。このことを「分極」していると呼ぶ。分極の程度が小さくなること、つまり膜電位が正の方向へと動くことを「脱分極」と呼ぶ。状況によっては、静止状態よりもさらに負側へと電位が変動することもあり。これは分極の程度が強くなるという意味で、「過分極」と呼ばれ、これらは細胞生理学でよく使われる用語である。

 1.5  Goldman-Hodgkin-Katzの式

実際の細胞では、複数のイオンが存在しそれぞれが異なる膜透過性を持つことから、静止膜電位とカリウム平衡電位が厳密に一致するわけではない。細胞膜中の電位勾配が一定であるという仮定のもとでは、カリウム、ナトリウム、塩素イオンを同時に考慮した平衡は、以下に示す Goldman-Hodgkin-Katzの式で与えられる。

ここで、P_K、P_NA、P_Cl はそれぞれのイオンの透過性の比を表す。

 2.　細胞膜の電気的性質

2.1　受動的性質

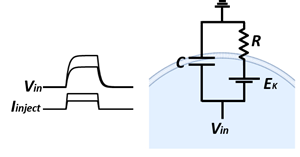
1.2項で述べたような微小電極を細胞内に二本刺入する。一つの電極で細胞膜電位を測りつつ、もう一方の電極からは細胞内に電流を注入することを考える。尚、工夫された電気回路を用いれば単一の電極で相当の実験を行うこともできる。矩形波型の電流注入に対して膜電位は静止膜電位から時間的に鈍った変化をする。これは1.1で述べたように細胞膜が抵抗と容量成分からなるためである。膜抵抗Rと膜容量Cの並列接続を細胞膜の簡単な等価回路と考える事ができる。定電流注入に対して膜電位は指数関数的に変化し、その時定数はに一致する。このような特性は細胞膜の受動的性質と呼ばれ、受動的性質のみを示す細胞は非興奮性細胞と呼ばれる。

図4　細胞膜の受動的性質と等価回路

 2.2　能動的性質

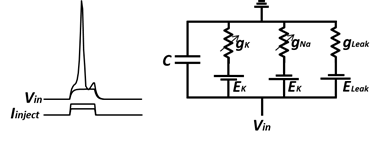
これに対し、神経や筋肉細胞のような興奮性細胞では、膜電位応答の振幅が小さいうちは受動的性質を示すものの、脱分極が一定の大きさ（閾値）に達するとスパイク状の膜電位変化が観察される。通常ピーク値は0 mVを超え+20～+60 mV程度に達する。持続時間は細胞の種類や状況によって異なるが、一般的な神経細胞では1～2ミリ秒、心室筋細胞では ~0.1秒程度である。このようなスパイク状の膜電位変化は活動電位 (action potential)と呼ぶ。インパルス（impulse）、発火（firing）などとよばれることもある。興奮性膜の等価回路は、図のように、受動膜のものを拡張し、各イオンの平衡電位に相当する電圧源と可変抵抗からなるものとして考えることができる。以下に説明するように、可変抵抗の抵抗値が膜電位と時間の関数として動的に変化するとすることにより、興奮成膜の特性が良く説明される。膜電位は容量C両端にかかる電圧に相当する。

図５　興奮成膜における能動的性質と等価回路

 

2.3　活動電位生成のイオン機序

外部入力により膜電位がある程脱分極すると、ナトリウムイオンの透過性が少し上昇する。これは分子レベルでは、細胞膜に存在する電位依存性ナトリウムチャネルの開口確率が上昇することに相当する。ナトリウムイオンのバランスは平衡からは大きくずれており、細胞外から内へと流入する。ナトリウムイオンは正電荷をもつので流入により膜電位はさらに正の方向へ変動し、その変動によりナトリウムイオンの透過性はさらに上昇する。このポジティブフィードバックにより膜電位はナトリウム平衡電位に向かって急峻に立ち上がる。このフィードバックはHodgkin サイクルとも呼ばれる。活動電位を起こす膜電位の「閾値」はこのサイクルが回り始める電位と言える。

このサイクルは一般的には次にように終焉する。膜電位とナトリウム平衡電位との「ずれ」が小さくなるにつれナトリウムイオンの流入速度は小さくなる。また、電位が上昇した状態において、開いたナトリウムチャネルは時間経過とともに閉じていく性質を持つ。これらに加え、時間的に遅れて電位依存性カリウムチャネルが開きだすことにより、膜電位はカリウム平衡電位付近に向かって急速に負側に戻る。膜電位が負に戻るとやがて電位依存性ナトリウムチャネルやカリウムチャネルは再び「閉じているが、また開ける」状態になる。すなわち、活動電位が再び発生するための環境が整う。

 2.4　 活動電位のイオン濃度への影響

イオンの流入出があると原理的には細胞内のイオン濃度が変化するはずであるが、どの程度であるかを見積もってみる。細胞膜の容量を1 μF/cm²とすると、半径r μmの球形の細胞の膜容量は  程度であるので、例えば膜電位を100 mV変化させるのに必要な電荷 である。ファラデー定数と細胞の体積から、が引き起こす濃度変化は、

であることがわかる。活動電位が生じてもナトリウムやカリウムイオンの濃度変化率は非常に小さいことが分かる。但し、カルシウムイオンは例外である。細胞内カルシウムイオンの濃度は非常に低く保たれているので、カルシウムイオンの流入が伴う場合には大きな濃度変化が起きる。カルシウムイオンは重要な細胞内シグナル伝達因子の一つとして機能する。

 

2.5　 Hodgkin-Huxley model

前述の活動電位が生成する仕組みは1950年代 Hodgkin, Huxleyらによるイカの神経軸索を用いた一連の実験により解明された。何故イカかというと、イカには直径1mm程度、長さは数cm以上に達する巨大な神経軸索をもつものがあり、細胞内液を置き換えたり2本の金属線電極を刺入して膜電位固定実験を行ったりと様々な操作が可能であったためである。Hodgkin-Huxley モデルは活動電位波形を定量的に説明することに初めて成功した現象論的なモデルである。イオンチャネルの存在が明らかになるずっと前に考案されたものであり、物質的実体を直接反映するものではないが、ナトリウムイオンとカリウムイオンが別の経路を透過することを仮定するなど、非常に高い先見性を備えていた。

Hodgkin-Huxley モデルでは、イオン透過性を制御するゲート粒子（gating particle）と呼ばれる仮想的な概念を考える。ゲート粒子はイオンが通過可能な状態（permissive state）と不可能な状態（non-permissive state）の二つの状態のみをとり、この状態間を遷移する。

alpha、beta は遷移速度で膜電位の関数でもある。mというゲート粒子を考え、permissive stateにある割合をmで表すと、

であるので、mは

に従って時間的に変遷する。

とおけば、

と書ける。すなわち、mは、時定数t_mでへと向かう。ただしこれらも膜電位に依存した変数である。膜電位が時間的に一定の場合、これらは定数となりｍは指数関数的にふるまう。同様に、mとは異なる特性で遷移するhゲート粒子も考える。

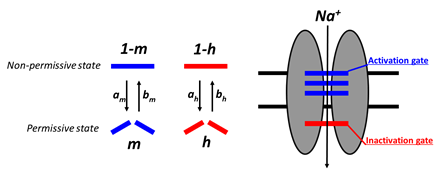（図6　Hodgkin-Huxley モデルにおけるナトリウム透過路）

Hodgkin-Huxley モデルにおいてナトリウム透過路はmゲート粒子3個とhゲート粒子が1つの合計４つのゲートで構成され、イオンが透過できるのは4つのゲートが全てpermissive stateにある時であり、その割合は、となる。ナトリウムイオン流出入による電流は、

で表せる。ここで、g_Naはすべてのゲートがpermissiveになったときに達成され得る最大コンダクタンス、Vは膜電位、E_Naはナトリウムイオンの平衡電位であり、V-ENa はイオン流入出を駆動する電圧（driving force）である。電流の符号に関しては、正電荷をもつイオンが細胞外から細胞内に流入する場合を負と定義する。

同様に、電位依存性なカリウムコンダクタンスはｎゲート粒子4つで構成され、カリウムイオンによる電流は次のように表現される。

またコンダクタンスが膜電位には依存しない漏洩電流

も考慮する。カリウムイオンの漏洩性については前述したが、クロライドイオンなどにも漏洩性があることが知られている。gleak, Eleak はこれらの漏洩成分を総合的にとらえたコンダクタンス及び平衡電位である。イオン電流はこれら三つの成分の総和として以下で表される。

細胞膜は容量を持つ。膜電位変化による容量性電流は

であるので、電流の総和は以下のようになる。

細胞内に電極を刺入する実験条件下で、電流の総和は電極を通じて計測器内部を通る電流に一致する。

電極を刺入していなければ、Itotal=0 となる。

このようにして、Hodgkin-Huxley モデルでは、V, m, h, nの４変数が、

に従って時間変化する。実験的に解析された a_m, b_m,, a_h, b_h,  a_n, b_n, を膜電位の連続関数としてフィッティングすると4変数の時間変化の数値計算が可能になる。Hodgkin, Huxleyらはこのようにして活動電位波形を良く再現できることを示した（文献3）。現在ではこのようなモデルを取り入れた神経細胞で大規模ネットワークを構成してその力学系としての挙動を調べたり、複雑な形態、多様なチャネル特性をもつ細胞の電気的特性などを解析したりするための計算環境も開発されている（文献4）。

 

2.6　興奮のより簡略されたモデル

Hodgkin-Huxley モデルは実際に観察されるような膜電位変化を良く再現するが、４つの変数が時間的に変動する複雑な構造をもつ。活動電位時におけるこれら４変数の挙動を調べると、ｖとｍは速く変化し、hとnは比較的ゆっくりと変動する。そこでHodgkin-Huxleyモデルを基礎にして、速い変数と遅い変数という2変数に落とし込んで簡略化した数理モデルが考案されている。FitzHugh-Nagumoモデル：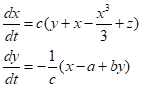

において、ｘは膜電位に相当する速い変数、ｙは不活性化を反映する遅い変数、a,b,cは定数で、ｚは外部からの入力で前述のI_electrodeに相当するパラメータである。定数を適切に設定することで、入力刺激に対する膜電位の振動など、実際の興奮性細胞で見られるものに定性的によく似た挙動を示す事が示され、理論的な側面からも様々な解析がされている。さらにNagumoにより、この力学系に相当する電子回路が実際に考案、作成されている。

 

3　膜興奮性を担う分子の実体

3.1　電位依存性イオンチャネル

イオン透過を担う物質としての実体はイオンチャネルと呼ばれる膜蛋白質群である。透過するイオンの種類、構造、機能など多様であり、遺伝子レベルでの差異なども含めれば極めて膨大な数になる。ここでは活動電位の発生において特に主要な役割を果たしている電位依存性ナトリウムチャネル及びカリウムチャネルの基礎的な性質や特徴を中心に触れる。

3.2　イオンチャネルの特徴

イオンチャネルの機能は、Neher、Sakmann らにより開発されたパッチクランプ法（文献5）により多くの知見が持たれされた。即ち、先端開口部が1～3 mm程度の微小ガラス管電極で細胞膜を吸引し、抵抗値にして1GΩ以上のシールを細胞膜と官壁との間に形成させることにより、微小な膜パッチに存在する単一イオンチャネルを通るイオン電流を解析することが可能になった。イオンチャネルには多様性があるので例外もあるが、原則的に以下の３つの特徴を備えている。

第一に、単一チャネルのコンダクタンスは離散的で、多くの場合において閉状態、開く状態の2状態である。開状態におけるコンダクタンスは、典型的には pSのオーダーである。

第２に、Hodgkin-Huxley モデルにおいてはコンダクタンスの時間変化が決定論的に考えられていたことに対して、実際のイオンチャネルチャネルの開閉は確率的で予測不能である（図7）。即ち、同じ膜電位変化に対して、単一チャネルの開閉が同じ挙動を示すことはない。細胞全体になるとイオン電流が画一的に見えるのは細胞膜全体の多数のチャネルを通るイオン電流がアンサンブル平均されることによる。したがって興奮性細胞においてHodgkinサイクルが回りだす膜電位である「閾値」という概念も、単一イオンチャネルのレベルになるとうまく当てはまらない。

第三は、一般的に高効率のイオン透過と高いイオン選択性を同時に兼ね備えていることである。ある種のカリウムチャネルでは、単一チャネルを自由拡散に近い速さである毎秒10⁷～10⁸個の割合でカリウムイオンが透過する一方で、よりイオン半径が小さいナトリウムイオンの透過性は10³～10⁴倍も低く抑えられている。

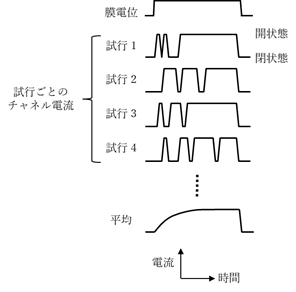図７　単一イオンチャネルの確率的な挙動。一般的な場合、時間はミリ秒、電流はピコアンペアのオーダーである。

 

3.3　イオンチャネルの構造

電位依存性ナトリウムチャネルは2000個以上のアミノ酸からなる大きさ10ナノメートル程度の蛋白質である。主たるαサブユニットはポリペプチドが６回細胞膜を貫通した構造を一単位として、それが4回連なった構造をしている（図８；文献6）。これに対して、カリウムチャネルの主要サブユニットのポリペプチドは６回膜貫通の構造一つのみを構成する。但しカリウムチャネルはそのサブユニットが4つ会合して構成されており、全体の構造は共通して24回膜貫通の構造となる。この他に補助的なβサブユニットなども存在し、チャネル全体の性質に影響を与えている。近年X線結晶構造やクライオ電子顕微鏡などにより詳細な分子構造が明らかなり、高いイオン選択性が実現されるメカニズムの理解などが進んでいる。

また、イオンチャネルは実社会との関連が深い生体分子群と言える。例えば、イオンチャネルの異常は家族性不整脈をはじめとする多くの疾患の原因であるほか、虫歯の治療の際によく用いられるリドカインなどの局所麻酔薬はナトリウムチャネルに結合して電気信号の発生を阻害することにより機能する。

図８　電位依存性ナトリウムチャネルの結晶構造（PDB#5VB2より）

3.3　活動電位の多様性を生むもの

細胞の種類によって活動電位の波形は大きく異なる。これは細胞種ごとに発現している電位依存性チャネルのプロファイル、密度や分布が異なるからである。電位依存性イオンチャネルの中でもカリウムチャネルは特に多様性が高いことで知られ、100種類以上の遺伝子群から構成される。また神経細胞などでは細胞の形態によっても細胞の電気特性が大きく変化することなども明らかとなっている。

これまで主にナトリウムとカリウムイオンによって活動電位生成を説明してきたが、ナトリウムイオンではなくカルシウムイオンが脱分極に関与している場合もある。フジツボの筋線維においてカルシウムイオンの細胞内への流入により活動電位が生じていることが知られている。また、心臓の拍動のペースメーカー信号を生成する洞房結節けるペースメーカー電位の立ち上がりもカルシウムイオンの流入が主要因である。

 

 4.　活動電位の伝播

 4.1　膜ケーブルの受動的特性

これまで細胞内を等電位とみなしてきたが、神経や筋細胞のように細胞が空間的に大きな広がりをもつ場合は発生した活動電位は空間的に伝播し得る。まず、無限長の円柱状の細胞膜で非興奮成膜の場合を考える。等電位とみなせる離散的な微小領域を考えることにより図９のような等価回路を考える事ができる。尚、細胞外領域にも実際には抵抗が存在して電位分布が生じるが、議論している膜電位に比べると十分に小さいのでここでは細胞外媒質の抵抗値は無視している。図の８回路は被覆された海底ケーブルの状況と等価であり、１８世紀末に大西洋横断ケーブル事業に関わっていたケルビンにより調べられたものである。r_a, , r_m, c_mを単位長さ当たりの抵抗や容量とすると、Vは、

に従う。この式はケーブル方程式ともいわれる。今、ある１点ｘ＝０に微小電極を刺して定電流を注入することにより、ｘ＝０における電位差がV_oとなるように保つことを考える。電流はr_aやr_mを通り細胞外におかれた参照電極へと流れる。定常状態では、

であり、となることが分かる。ここでは長さ定数と言われ、減衰の程度を示す指標である。R_a, R_mを細胞内媒質、脂質膜の単位面積当たりの抵抗、円柱断面の直径をDとすれば、

となり、円柱が太いほど遠くまで広がる。実際の細胞環境における長さ定数は数mm程度に相当する。また、c_mの効果を考えてみると、注入した電流のうちが容量の充電に用いられるため、大きなc_mは定常状態への到達時間を長くする。このように細胞が空間的広がりを持つ場合、受動的性質により細胞内にこの細胞の形状によって細胞内電位に空間分布が生じる。また通常の大きさ数十マイクロメートル以下の細胞体であれば、細胞内部は等電位であるとみなして良いことも解る。

図９　受動的ケーブル膜の等価回路

 

4.2　膜ケーブルの能動的性質

神経細胞の軸索のように興奮性膜であり受動的性質に加え能動的性質が加わる場合を考える。ある部位にて活動電位が発生したとする。4.1で見たような効果により空間的な膜電位の広がりが生じる。Hodgkin サイクルがまだ回っていなかった領域でも膜電位が閾値に達し、サイクルが回り始め、活動電位が生じる。このようなプロセスにより活動電位は自己再生的に伝播し、このような様式は興奮伝導とも呼ばれる。

数理的に考察するには、ケーブル方程式とHodgkin-Huxley モデルを組み合わせた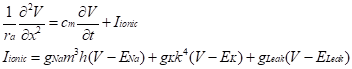

を考えればよいが、解析的な扱いは難しい。数値計算により、あるパラメータのものでは一定速度で空間的に同じ形の活動電位が伝播することが示されている。また、伝導速度には太さと

の関係があることが示され、受動的性質における長さ定数λに対する相関と同じであることがわかる。鈍痛や冷感を中枢方向へと伝達するC線維と呼ばれる神経線維は、太さ0.5 mm程度、伝導速度は1 m/s程度であることが知られている。これに対し、イカの巨大軸索は太さ0.5 mm程度、速度は25 m/s以上に達する。しかしながら、伝導速度を速める為にケーブル径を太くすることは、スペースをとり集積化に適さない他、イオン環境の維持に必要なエネルギーが増加してしまうなどのディメリットがある。

 

4.3　跳躍伝導

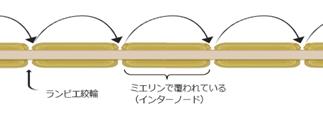
有髄線維とよばれる神経軸索では巧みな機構により伝導速度が飛躍的に高められている。有髄線維では軸索部がミエリンとよばれる脂質膜で多重に覆われ、そのなかで1~2 mmおきにミエリンで囲まれない1 mm程度の間隙が存在する。この間壁はランヴィエ絞輪と呼ばれる（図１０）。

ミエリンで覆われる軸索部に電位依存性ナトリウムチャネルはほとんど存在せず、受動膜としてふるまう。この部位はミエリンで覆われるため r_mが大きく、したがって長さ定数が長い。また、c_mは小さくなることから、膜電位は速く、なおかつ遠くまで伝播することが分かる。ランヴィエ絞輪部の軸索の膜には電位依存性チャネルが集積し、活動電位が生じる。このようにして膜電位はミエリン部を高速に受動的に伝播し、以降のランヴィエ絞輪部で次々と活動電位が生じる。この様式は跳躍伝導と呼ばれる。生体においては多くの神経がこのような有髄繊維であり、例えば、中枢から骨格筋への信号伝達を担うAa線維は太さ15 mm程度ながら伝導速度は100 m/sに達する。

図１０　跳躍伝導の模式図

 5.　隣接細胞への信号伝達

5.1　化学シナプス

活動電位が軸索末端の隣接細胞と近接したシナプスと呼ばれる部位に到着すると細胞内カルシウムイオンの上昇を介して神経伝達物質が放出される。伝達物質はシナプス間隙を拡散し隣接細胞の膜にある受容体と結合する。イオンチャネル型の受容体は、結合とともにイオンチャネルの開口確率が上昇し、イオンの流入出を引き起こす。脱分極方向に作用する場合を興奮性、過分極方向に作用する場合を抑制性のシナプス伝達と呼ばれる。運動ニューロン-骨格筋のシナプスの場合、伝達物質はアセチルコリンで脱分極を引き起こす。骨格筋で活動電位が生じるとカルシウムイオンが細胞内の小胞から放出する機構が働き、筋収縮へと至る。神経細胞間のシナプスではグルタミン酸やγアミノ酪酸などが主要な伝達物質である。神経細胞の活動履歴などに応じてシナプスの伝達効率は動的に変化する事が知られており、学習や記憶の素過程であると考えられている。

 

5.2　ギャップ結合

蛋白質コネキシンが集合してできるコネクソンと呼ばれる円柱型の構造体を介して隣接する細胞間を伝播する様式もある。コネクソン中心部をイオンが通過できることにより隣接する細胞は電気的に連結される。ギャップ結合とも呼ばれる。特に心筋細胞などで顕著にみられ、心房や心室が機能的なシンシチウムとして同期して活動するのに重要な役割をもつ。このほか、網膜神経細胞間などにおいてもギャップ結合を介した信号伝達がみられる。

6. 細胞外媒質に現れる電位分布

 6.1　細胞外から観る細胞の電気活動

これまでは細胞外を等電位とみなし、細胞膜内外の電位差の生成や時空間伝播を考えてきた。では、例えば脳波や心電図のように、両方ともが細胞外に置かれた電極間に細胞の電気活動を反映した電位差が生じるのはどうしてだろうか？

これまでの議論では細胞外媒質の抵抗を無視していなかったが、実際の抵抗値は当然ながら有限な値を持つ。例えば、血液の体積抵抗率は150 Ωcm程度とされる。細胞の（特に集団的な）電気活動により、電気的中性が崩れた微小領域が細胞の電気活動により媒質中に出現する結果、細胞外には媒質の伝導率σに応じた電位差の時空間的な分布が生じることになる。しなしながら、任意の２点間の電位差はは系を構成するすべての部位の電荷分布を反映するので、第一原理（ガウスの法則）をもとに、細胞外電極で観察される信号を細胞の微視的な現象と密接に関連させて理解することは困難である。従って計測としての厳密性を追求するよりも、より柔軟な枠組みのもと、その非侵襲性を活かして細胞集団や組織、器官レベルの巨視的な情報を得ることや、それらを診断や外部制御に用いることなどの実利に重きがおかれる傾向にある。

 

6.2　細胞外から観測される信号の解釈と利用

脳波や神経細胞の細胞外記録を考える上でよく用いられる概念に点電流源（point current source）がある。簡単に伝導率σが等方的であるとする。媒体中の点電流源Ｉがそこからdの距離に形成する電位φは

で与えられる。この関係式は、マクスウェル方程式から出発していくつかの仮定を置くことにより得られる。点電流源の概念においてＩはベクトルではなくスカラー量である。詳細は正書（文献４など）を参考にされたい。媒質中に形成される電位φは、各々の点電流源のつくる電位の総和であり、

となる。小さな球形細胞で活動電位が生じたとしよう。であるので原理的には点電流源Ｉは生じない。点電流源が生じるのは、細胞内外の媒質を電流が空間的に広がって流れる場合である。簡単な1次元ケーブルの場合を当てはめて考えると、ケーブル方程式より

であるので、媒質中に形成される電位とは膜電位の空間分布を反映したものと考えることができる。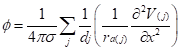

金属微小電極を単一の神経細胞に接近させて遠くに置かれた参照電極との電位差を測ると、1/dの効果により、実質的にその単一細胞のみの活動を反映した電位変化を計測することができる。これは単一ユニット記録と呼ばれる。より太くて低インピーダンス（数百kΩ程度）の電極を用いると、計測される電位は神経細胞の集団活動を反映したものとなり、局所フィールド電位と呼ばれる。しばしば、多点計測されたれた局所フィールド電位信号を用いて、脳内の電流源の分布解析が行われる。電流源密度推定法とよばれ、様々な数理手法が考案されている。そして頭皮上に置かれた電極を用いてより非侵襲的に神経細胞の集団活動を測定するものが脳波記録（EEG）である。脳波記録はその非侵襲性から多数の電極をもちいた多点計測への拡張が比較的容易である。

一方、心筋細胞の活動に伴う体表電位変化を計測することを目的としたものが心電図（ECG、EKG）である。体表電位変化の物理的な生成要因は神経細胞に由来する場合と変わりないものの、その解釈には「心ベクトル」と呼ばれる概念が古くから用いられている。心ベクトルとは心臓を構成する多数の心筋細胞の電気状態をアンサンブル的に1本のベクトルで表現したものであり、定められた12種類の誘導法は心ベクトルを様々な角度に投影し、その成分を見ていると考えるモデルである。電気軸と呼ばれる心ベクトルの体軸に対する角度を見積もることにより、例えば心室肥大などの潜在的なリスクの発見に役立つことなどが知られている。同様に、皮膚貼り付け電極など用いて主として骨格筋の筋線維の活動電位を反映する信号を測るの筋電図（EMG）や、視細胞、網膜内細胞、神経節細胞などの網膜構成細胞の電気活動を主な計測対象とする網膜電図（ERG）なども同様に細胞活動によって生じる細胞外の電位分布を測るものであり、組織の生理機能の診断のみならず、様々な外部デバイスを駆動するための信号源として用いる試みが盛んに行われている。

(参考文献）

1. 標準生理学　医学書院
2. Voet, Voet. “Biochemistry”. Section 20-3, p. 759
3. HODGKIN, A.L., & HUXLEY, A.F. (1952). The Journal of physiology, 117(4), 500-44
4. https://neuron.yale.edu/neuron/
5. Electric Fields of the Brain: The Neurophysics of EEG, Paul L. Nunez, Ramesh Srinivasan, Oxford Univ. Press