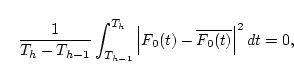 )
in constraint (i).
In this assumption, Ak(t) which can be allowed to undergo a temporal change in region, constrains the second-order polynomial (
)
in constraint (i).
In this assumption, Ak(t) which can be allowed to undergo a temporal change in region, constrains the second-order polynomial (
In this paper, in order to reduce the computational cost for estimating
Ck,R(t) and
Dk,R(t), we assumes that
Ck,R(t) is a linear (R=1) polynomial (
dAk(t)/dt=Ck,1(t)) and
Dk,R(t) is zero (
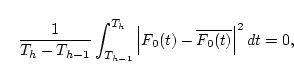 )
in constraint (i).
In this assumption, Ak(t) which can be allowed to undergo a temporal change in region, constrains the second-order polynomial (
)
in constraint (i).
In this assumption, Ak(t) which can be allowed to undergo a temporal change in region, constrains the second-order polynomial (
![]() ).
Moreover,
).
Moreover,
![]() ,
which is constrained (i.e.
,
which is constrained (i.e.
![]() ), cannot be allowed to temporarily change.
Here, if the number of channels K is very large, each frequency of the signal component that passed through the channel approximately coincides with the center frequency of each channel.
Even if the above condition is false, its frequency difference can be represented by Dk,0.
), cannot be allowed to temporarily change.
Here, if the number of channels K is very large, each frequency of the signal component that passed through the channel approximately coincides with the center frequency of each channel.
Even if the above condition is false, its frequency difference can be represented by Dk,0.
In the segment
Th-Th-1,
Ck,1(t) and Dk,0 are determined by the following steps.
First, let Dk,0 be any value within
![]() .
Next, using the Kalman filter, determine the estimated region,
.
Next, using the Kalman filter, determine the estimated region,
![]() ,
where
,
where
![]() is the estimated value and Pk(t) is the estimated error.
Then select candidates of
Ck,1(t) using the spline interpolation in the estimated error region.
Next, determine
Ck,1(t) using
is the estimated value and Pk(t) is the estimated error.
Then select candidates of
Ck,1(t) using the spline interpolation in the estimated error region.
Next, determine
Ck,1(t) using
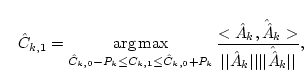 is obtained by the spline interpolation and
is obtained by the spline interpolation and
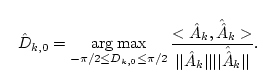 and
and