| (15) |
In the proposed model, the fundamental frequency F0(t) is estimated using Comb filtering on the auditory-motivated filterbank.
This Comb filter is defined by
| (15) |
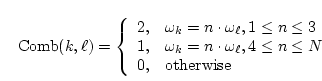 are indices,
are indices, | (16) |
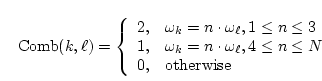 .
The estimated F0(t) is determined by
.
The estimated F0(t) is determined by
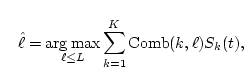 .
.
Since the number of channels in the auditory-motivated filterbank is finite, the estimated fundamental frequency F0(t) takes a discrete value.
In addition, the fluctuation of the estimated F0(t) behaves like a stair shape and the temporal differentiation of F0(t) is zero at any segment.
Therefore, this paper assumes that
E0,R(t)=0 in constraint (ii) for a segment.
Here, the above segment is determined using the following equation, as the duration for which the temporal variation of F0(t) has variance of zero as F0(t).