


Next: Calculation of the four
Up: Model A: Auditory segregation
Previous: Auditory filterbank
First, we can observe only the signal f(t), where
f(t)=f1(t)+f2(t),
f1(t) is the desired signal and f2(t) is a noise masker.
The observed signal f(t) is decomposed into its frequency components by an auditory filterbank.
Second, outputs of the k-th channel, which correspond to f1(t) and f2(t), are assumed to be
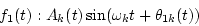 |
(2) |
and
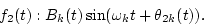 |
(3) |
Here, 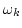 is the center frequency of the auditory filter and
is the center frequency of the auditory filter and
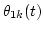 and
and
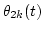 are the input phases of f1(t) and f2(t), respectively.
Since the output of the k-th channel Xk(t) is the sum of Eqs. (
are the input phases of f1(t) and f2(t), respectively.
Since the output of the k-th channel Xk(t) is the sum of Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ),
),
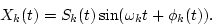 |
(4) |
Therefore, the amplitude envelopes of the two signals Ak(t) and Bk(t) can be determined by
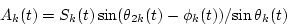 |
(5) |
and
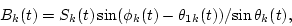 |
(6) |
where
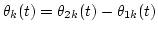 and
and
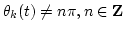 .
Since the amplitude envelope Sk(t) and the output phase
.
Since the amplitude envelope Sk(t) and the output phase  are observable, then if
are observable, then if
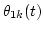 and
and
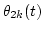 are determined, Ak(t) and Bk(t) can be determined by the above equations.
Finally, all the components are synthesized from Eqs. (
are determined, Ak(t) and Bk(t) can be determined by the above equations.
Finally, all the components are synthesized from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and (
) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) in the grouping block.
Then f1(t) and f2(t) can be reconstructed by the grouping block using the inverse wavelet transform.
Here,
) in the grouping block.
Then f1(t) and f2(t) can be reconstructed by the grouping block using the inverse wavelet transform.
Here,
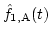 and
and
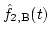 are the reconstructed f1(t) and f2(t), respectively.
are the reconstructed f1(t) and f2(t), respectively.
In this paper, we assume that the center frequency of the auditory filter corresponds to the signal frequency.
Therefore, we consider the problem of segregating f1(t) from f(t) when
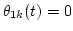 and
and
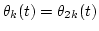 .
.



Next: Calculation of the four
Up: Model A: Auditory segregation
Previous: Auditory filterbank
Masashi Unoki
2000-10-26
![]() and
and
![]() .
.