Auditory filterbank

An auditory filterbank is constructed using the wavelet transform, where the basic function 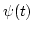$\psi(t)$ is the impulse response of the gammatone filter [8] which is represented using the Hilbert transform.

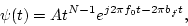$$\psi(t)=At^{N-1}e^{j2\pi f_0 t-2\pi b_f t},$$ (1)

where ERB (f₀)=24.7(4.37f₀/1000+1) and b_f=1.019ERB(f₀). This is a constant Q filterbank whose a center frequency f₀ is 1 kHz, a bandpassed region from 100 Hz to 10 kHz, and number of channel of 128; the bandwidth of the auditory filter is 1 ERB. In addition, we compensate for the group delay by adjusting the peak in the envelopes of Eq. () for all scale parameters, which is called ``alinement processing,'' because the group delay occurs for each scale.