Stimuli and procedure

To consider conditions equivalent to the experimental ones used by Hall et al., in this simulation we assume that f₁(t) was a sinusoidal signal , where a center frequency was 1 kHz, duration was 400 ms and the amplitude envelope was constant, and that f₂(t) was two types of bandpassed noise masker having center frequency close to the signal frequency. In addition, we adjust the bandwidths of the auditory filters, which is equivalent to the masker bandwidth, in stead of the two maskers made by fixing the masker bandwidth to 1 kHz. One was a bandpassed random noise f₂₁(t) and other was an AM bandpassed random noise f₂₂(t). This masker was amplitude modulated f₂₁(t), where the modulation frequency was 50 Hz and the modulation rate was 100%. Here, the power of the noise masker f₂(t) was adjusted so that $\sqrt{f_{21}(t)^2/f_{22}(t)^2}=1$. Moreover the power ratio between f₁(t) and f₂(t), i.e., the SNR (signal-to-noise ratio), was -6.6 dB.

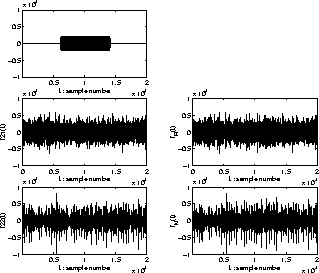
In this simulation, the mixed signals were f_R(t)=f₁(t)+f₂₁(t) and f_M(t)=f₁(t)+f₂₂(t), corresponding to the stimuli labeled R and M, respectively. Simulation stimuli consisting of 10 sinusoidal signals were formed by varying the onset and 30 maskers of two types were formed by varying random seeds. Thus, the total number of stimuli was 300. As an example, one of the two types of mixed signals is shown in Fig. . Here, a sinusoidal signal f₁(t) is masked visually in the all-mixed signal, but we can hear the sinusoidal signal from f_M(t) because of the CMR; however, we cannot hear the sinusoidal signal from f_R(t) because of the masking.

  

Figure: Stimuli: a sinusoidal signal f₁(t) (left-top), a bandpassed random noise f₂₁(t) (left-middle), and an AM bandpassed noise f₂₂(t) (left-bottom). Mixed signals f_R(t) (right-top) and f_M(t) (right-bottom).

In this paper, we set the parameters for $\Delta t=3/(f_0\cdot \alpha^{k-\frac{K}{2}})$, $\Delta A=\vert A_k(T_r-\Delta t)-A_k(T_r-2\Delta t)\vert$, $\Delta B=0.01S_{\max}$, and $\Delta \theta=\pi/20$, where $S_{\max}$ is the maximum of S_k(t).

In their demonstration of CMR, Hall et al. measured the masking threshold as a function of the masker bandwidth. Our simulation conditions can be considered to be the same as the experimental ones used by Hall et al. since we measured the SNR of the extracted sinusoidal signal $\hat{f}_{1,A}(t)$ as a function of the number of adjacent auditory filters L, which is equivalent to the masker bandwidth, where the masker bandwidth is fixed. Therefore, $\theta_{2k}(t)$ is uniquely determined by the amplitude envelope $\hat{\hat{B}}_k(t)$ as a function of L from Eqs. (), (), and (). The bandwidths related to L=1, 3, 5, 7, 9, 11 are 207, 352, 499, 648, 801, 958 Hz, respectively.