 |
 |
The results of simulations for the two models show that model A simulates the phenomenon of CMR/simultaneous masking by coherence/incoherence between the fluctuations of amplitude envelope of a masker when the masker bandwidth increases above 1 ERB.
Moreover, model B simulates the phenomenon of simultaneous masking in which the threshold increases as a function of the masker bandwidth as the masker bandwidth increases up to 1 ERB and then the threshold remains constant.
The selection process therefore selects the lowest of these masking thresholds.
In other words, it selects the highest SNR of the signal extracted from
![]() and
and
![]() ,
and let
,
and let
![]() be the extracted signal with the highest SNR.
Thus, from Figs.
be the extracted signal with the highest SNR.
Thus, from Figs. ![]() and
and ![]() the proposed model has the characteristics of the masking threshold shown in Fig.
the proposed model has the characteristics of the masking threshold shown in Fig. ![]() .
In the selection process, the extracted signal with the lowest threshold is selected from the signals extracted using the two models.
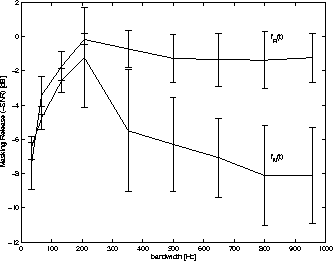
These characteristics show that the phenomenon of CMR is similar to Hall et. al.'s results.
Hence, it can be interpreted that the proposed model is a computational model of CMR.
The maximum amount of CMR in Hall et al.'s demonstrations was about 10 dB.
In contrast, the maximum amount of CMR in our model was about 8 dB.
.
In the selection process, the extracted signal with the lowest threshold is selected from the signals extracted using the two models.
These characteristics show that the phenomenon of CMR is similar to Hall et. al.'s results.
Hence, it can be interpreted that the proposed model is a computational model of CMR.
The maximum amount of CMR in Hall et al.'s demonstrations was about 10 dB.
In contrast, the maximum amount of CMR in our model was about 8 dB.