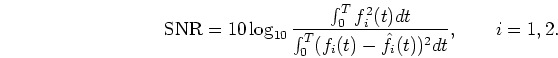 in physical constraint 3
is determined by
in physical constraint 3
is determined by
We will consider as experimental stimuli ten pairs of two types of
mixed signals used in previous section, fM(t) and fR(t).
Although the simulation for CMR [19] was carried out for a
function of the bandwidth of noise, this simulation is carried out for
a function of a number of adjacent auditory filters L related to the
bandwidth of a bandpassed noise.
The amplitude envelope
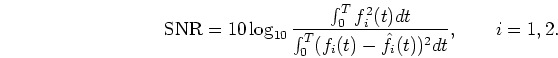 in physical constraint 3
is determined by
in physical constraint 3
is determined by
| (31) |
Relationship between the bandwidth and the improved SNR is shown in
Fig. ![]() .
In this figure, the vertical axis shows inversely the improved SNR of
a sinusoidal signal and the horizontal axis shows the bandwidth in
relation to L.
The real line and the error-bar show mean and standard deviation of
the SNR, respectively.
It was shown that, for the mixed signal fM(t), the SNR of
sinusoidal signal
.
In this figure, the vertical axis shows inversely the improved SNR of
a sinusoidal signal and the horizontal axis shows the bandwidth in
relation to L.
The real line and the error-bar show mean and standard deviation of
the SNR, respectively.
It was shown that, for the mixed signal fM(t), the SNR of
sinusoidal signal
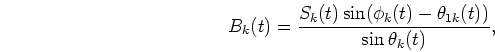 can be improved as the number of
adjacent auditory filters L increase.
In contrast, it is shown that, for the mixed signal fR(t),
can be improved as the number of
adjacent auditory filters L increase.
In contrast, it is shown that, for the mixed signal fR(t),
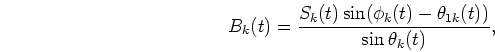 cannot be improved as L increases.
Here, improvement of the extracted sinusoidal signal is equivalent to
masking release.
These results show that the masking of a sinusoidal signal can be
released as a function of the bandwidth of bandpassed noise when noise
is AM banpassed noise, and that it cannot be released as a function of
the bandwidth when noise is bandpassed random noise.
For reasons, the proposed model can be interpreted as a computational
model of CMR.
cannot be improved as L increases.
Here, improvement of the extracted sinusoidal signal is equivalent to
masking release.
These results show that the masking of a sinusoidal signal can be
released as a function of the bandwidth of bandpassed noise when noise
is AM banpassed noise, and that it cannot be released as a function of
the bandwidth when noise is bandpassed random noise.
For reasons, the proposed model can be interpreted as a computational
model of CMR.