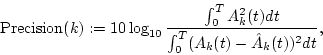 |
(11) |
We carried out two simulations on segregating two-acoustic sources using noise-added signal f(t) to show that the proposed method can extract the desired signal f1(t) from it. The two simulations are composed as follows:
We use two types of measures to evaluate the performance of the segregation using the proposed method.
One is the power ratio in terms of the amplitude envelope Ak(t), i.e., the likely SNR.
The aim of using this measure is to evaluate the segregation in terms of the amplitude envelope where signal and noise exist in the same frequency region.
This measure is called ``Precision,'' and is defined by
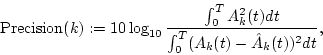 |
(11) |
The other is spectrum distortion (SD).
The aim of using this measure is to evaluate the extraction of a desired signal
![]() from noise-added signal f(t).
This measure is defined by
from noise-added signal f(t).
This measure is defined by
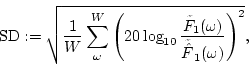 |
(12) |
The reduced SD of f1(t) is the SD difference between f(t) and
![]() .
.