


Next: Calculation of the four
Up: Auditory segregation model
Previous: Auditory segregation model
In this paper, we define the problem of segregating two acoustic sources as ``the segregation of the mixed signal into original signal components, where the mixed signal is composed of two signals generated by any two acoustic sources.''
We formulate it as follows:
Firstly, we can observe only the signal f(t):
where f1(t) is the desired signal and f2(t) is a noise.
The observed signal f(t) is decomposed into its frequency components by an auditory filterbank.
Secondly, outputs of the k-th channel, which correspond to f1(t) and f2(t), are assumed to be
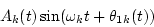 |
(2) |
and
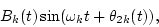 |
(3) |
respectively.
Since the output of the k-th channel Xk(t) is represented by
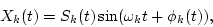 |
(4) |
where
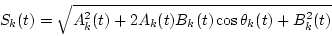 |
(5) |
and
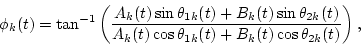 |
(6) |
then the amplitude envelopes of the two signals Ak(t) and Bk(t) can be determined by
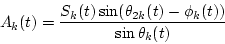 |
(7) |
and
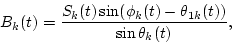 |
(8) |
respectively, where
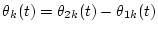 and
and
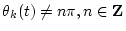 .
Thus, if the four parameters, Sk(t),
.
Thus, if the four parameters, Sk(t), 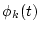 ,
,
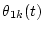 ,
and
,
and
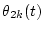 are calculated, Ak(t) and Bk(t) can be calculated by the above equations.
Finally, f1(t) and f2(t) can be reconstructed by grouping constraints.
are calculated, Ak(t) and Bk(t) can be calculated by the above equations.
Finally, f1(t) and f2(t) can be reconstructed by grouping constraints.
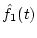 and
and
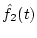 are reconstructed f1(t) and f2(t), respectively.
are reconstructed f1(t) and f2(t), respectively.
In this paper, we assume
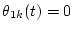 and
and
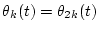 .
Additionally, we consider the problem of segregating two acoustic sources in which the localized f1(t) is added to f2(t).
.
Additionally, we consider the problem of segregating two acoustic sources in which the localized f1(t) is added to f2(t).



Next: Calculation of the four
Up: Auditory segregation model
Previous: Auditory segregation model
Masashi Unoki
2000-10-26
![]() and
and
![]() .
Additionally, we consider the problem of segregating two acoustic sources in which the localized f1(t) is added to f2(t).
.
Additionally, we consider the problem of segregating two acoustic sources in which the localized f1(t) is added to f2(t).