file=FIGURE/basicmodel.eps,width=0.47
![% latex2html id marker 2081
\fbox{\footnotesize{
\begin{minipage}[h]{7.5cm}
\beg...
...ref{eq:B_k});
\end{tabbing}\end{minipage}}}
\par \caption{Segregation algorithm}](img60.gif)
decompose f(t) into its frequency components using the
wavelet filterbank (wavelet transform) as Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
for k:=1 to K do
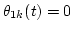 and
and 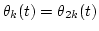 ; ;
determine Sk(t) and 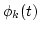 from Lemma 1;
from Lemma 1;
determine onset 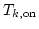 and offset
and offset 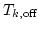 ; ;
the segregated duration is 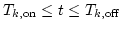 ; ;
if Physical constraint 4 or 5 is satisfied 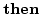
estimate Ck(t) using the Kalman filter;
determine the interpolated duration;
let I be the number of the interpolated samples;
for i=1 to I do
determine the candidates for Ck(t), which
interpolated by the spline function within
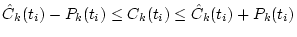 ; ;
determine 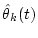 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
determine 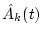 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
determine 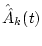 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
determine 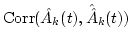 from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
end
determine Ck(t) when 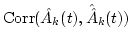
becomes a maximum within the estimated
-error;
determine  from Eq. (
from Eq. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
else
set Ak(t)=0, Bk(t)=Sk(t) and 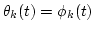 ; ;
end
determine Ak(t) and Bk(t) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and ( ) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
determine each frequency components of f1(t)
and f2(t) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and ( ) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
end
reconstruct 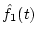 and
and 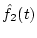 using the wavelet filterbank
using the wavelet filterbank
(inverse wavelet transform) from Eqs. (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ) and ( ) and (![[*]](/usr/share/latex2html/icons.gif/cross_ref_motif.gif) ); );
|
![]() ) is the wavelet transform given by Eq. (
) is the wavelet transform given by Eq. (![]() ) as follows.
) as follows.
![]() ) and (
) and (![]() ),
we obtain the following relation.
),
we obtain the following relation.