Simulation 2

      

Figure: Two AM complex tones, f₁(t) and f₂(t).
Figure: Mixed signals f(t).
Figure: SD for $\hat{f}_1(t)$ and the reduced SD of $\hat{f}_1(t)$.

This simulation assumes that f₁(t) is an AM complex tone as the same as Fig. and f₂(t) is another AM complex tone as shown in Fig. , where F₀=300 Hz, N_F0=10, and whose amplitude envelope is sinusoidal (15 Hz). Therefore, harmonics of f₁(t) and f₂(t) in the multiple of 600 Hz, for example, third harmonic of f₁(t) and second harmonic of f₂(t), exist in the same frequency region. Seven types of f(t) are used as simulation stimuli, where the SNRs of f(t) are from -10 to 20 dB in 5-dB steps. 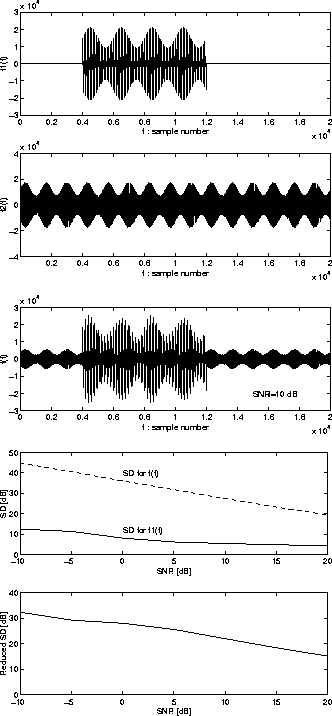Mixed signal in case of SNR=10 dB is plotted in Fig. .

    

Figure: Precision for A_k(t) (SNR=10 dB).
Figure: Extraction property for $\hat{f}_1(t)$ (SNR=10 dB).

The simulations were carried out using the seven mixed signals. The average SDs of f₁(t) and f(t) , and the mean of the reduced SD of f₁(t) are shown in Fig. . Hence, it is possible to reduce the SD by about 20 dB as noise reduction, using the proposed method. For example, when the SNR of f(t) is 10 dB, the proposed method can segregate A_k(t) with a high precision as shown in Fig. , and can extract the $\hat{f}_1(t)$ shown in Fig. from the f(t) as shown in Fig. . Hence, just as the result of previous simulations, the proposed model can also extract the amplitude information of signal f₁(t) from a noise-added signal f(t) with a high precision in which two AM complex tones exist in the same frequency region.