


Next: Bibliography
Up: Vowel segregation in background
Previous: Conclusions
The authors wish to thank H. Kawahara of Wakayama University and T. Irino of ATR-HIP for helpful suggestions about this work, and Y. Ichinose and S. Katagiri of ATR-HIP for the arrangement.
This work was supported by a Grant-in-Aid for science research from the Ministry of Education (Research Fellowships of the Japan Society for the Promotion of Science for Young Scientists and No. 10680374) and by CREST (Core Research for Evolutional Science and Technology) of Japan Science and Technology Corporation (JST).
Table:
Definitions of symbols for Kalman filtering
| Symbol |
Est. of Bk(t) |
Est. of
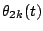 |
Est. of
Ck,0(t) |
Est. of
Dk,0(t) |
Observed signal
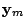 |
Xk(tm) |
 |
Xk(tm) |
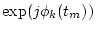 |
State variable
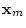 |
Bk(tm) |
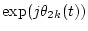 |
Ck(tm) |
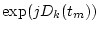 |
Observed noise
 |
X1,k(tm) |
X1,k(tm)/Sk(tm) |
X2,k(tm) |
X2,k(tm)/Sk(tm) |
System noise
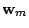 |
wm |
wm |
wm |
wm |
State transition matrix
 |
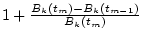 |
 |
 |
 |
Observation matrix
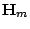 |
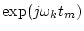 |
Bk(tm)/Sk(tm) |
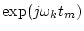 |
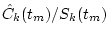 |
Driving matrix
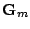 |
1 |
1 |
1 |
1 |
Initial value
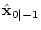 |
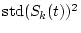 |
 |
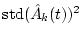 |
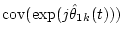 |
Initial value
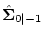 |
Sk(t0) |
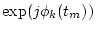 |
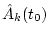 |
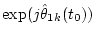 |



Next: Bibliography
Up: Vowel segregation in background
Previous: Conclusions
Masashi Unoki
2000-11-07