In this paper, it is assumed that the desired signal f1(t) is a harmonic tone, consisting of the fundamental frequency F0(t) and the harmonic components, which are multiplies of F0(t).
The proposed model segregates the desired signal from the mixed signal by constraining the temporal differentiation of the instantaneous amplitude Ak(t), the instantaneous phase
![]() ,
and the fundamental frequency F0(t).
Constraints used in this model are shown in Table 1.
Constraint (ii) for the above parameters gives
dAk(t)/dt=Ck,R(t),
,
and the fundamental frequency F0(t).
Constraints used in this model are shown in Table 1.
Constraint (ii) for the above parameters gives
dAk(t)/dt=Ck,R(t),
![]() ,
and
dF0(t)/dt=E0,R(t), where
Ck,R(t),
Dk,R(t), and
E0,R(t) are R-th-order differentiable piecewise polynomials (using Table 1 (ii)).
Then, substituting
dAk(t)/dt=Ck,R(t) into Eq. (
,
and
dF0(t)/dt=E0,R(t), where
Ck,R(t),
Dk,R(t), and
E0,R(t) are R-th-order differentiable piecewise polynomials (using Table 1 (ii)).
Then, substituting
dAk(t)/dt=Ck,R(t) into Eq. (![]() ), we get the linear differential equation of the input phase difference
), we get the linear differential equation of the input phase difference
![]() .
By solving this equation, a general solution is determined by
.
By solving this equation, a general solution is determined by
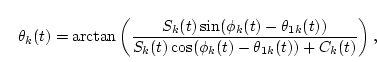 .
.