どんな分割でも良いなら，実に多数の三角形分割が可能であることが知られています．具体的には，nの指数関数通りもの多数の分割方法があります．このように平面のある部分を三角形のような基本図形だけで埋め尽くしたものをメッシュと呼びますが，有限要素法など様々な場面で使われています．多数ある三角形分割の中で，構成三角形の中に非常に小さな内角をもつものがあれば，それは非常にひしゃげた形をしているので，有限要素法などの計算において計算誤差を生じやすいことが知られています．そこで，内角の最小値が最大であるような三角形分割を求めたいという要求が起こります．そのような三角形分割のことをデローネイ三角形分割と言います.下に示したのはデローネイ三角形分割の例です．

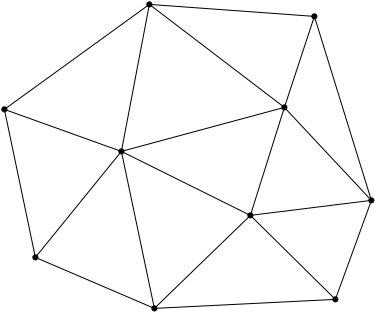
　このような三角形分割が与えられたとき，これが最小の内角を最大化しているかどうかを検証することは容易ではありません．しかし，幸運にも，三角形分割の場合には数学的に良い性質が知られています．それは，どの三角形をとっても，その三角形の外接円の内部に他の点は一切含まれないという性質です．もしこの性質が成り立つなら，最小角が最大になっていることを数学的に証明することができます．ある三角形に外接する円の内部に他の点が存在するかどうかは単純な方法でO(n)の時間で調べることができます．三角形の個数も高々 n であることも証明できるので，与えられた三角形分割が上記の空円に関する条件を満たすかどうかは n の2乗に比例する時間で調べることができます．
　実は，分割統治法を用いることでデローネイ三角形分割をO(n log n)の時間で構成するアルゴリズムが知られています．計算幾何学の分野では常識となっているアルゴリズムなのですが，実際にプログラムとして実装しようとすると，データ構造も面倒で，なかなか一朝一夕に実装できるものではありません．実際，私も若いときに実装を試みましたが，データ構造が面倒で，結局，実装を断念しました．複雑なデータ構造を使うぐらいですから，作業領域もO(n)だけ必要です．
　では，定数個の変数だけを使ってデローネイ三角形を求めることはできるでしょうか．すべての3点の組み合わせについて，対応する三角形の外接円が空円かどうかを判定し，空円ならばデローネイ三角形だとして出力するという単純な方法を用いることで，確かにデローネイ三角形分割を描くことは出来ます．しかし，この単純な方法では n の4乗に比例する時間がかかってしまうので，もっと高速のアルゴリズムが存在するかに関心があります．
　結果から先に言うと，定数個の変数を使うだけで，n の2乗に比例する時間でデローネイ三角形分割を計算するアルゴリズムが得られています．2009年にカナダの国際会議で発表したものです．簡単に言うと，すべての点について同じ操作を行います．点 p については，まず p に最も近い点 q をO(n)の時間で求めます．このとき，線分 pq はデローネイ三角形の辺になっていることを証明することができます．三角形にするためにもう1点 r が必要ですが，3点 p, q, r で定まる円が空円でなければならないという性質を用います．具体的には，他のすべての点 r について，三角形 pqr の外接円の半径を計算します．半径が最小であるような点 r が求める点です．したがって，O(n)の時間で最初の三角形を求めることができました．次に，線分 pq の代わりに線分 pr を用いて，それと共に空円を構成できる3点目をやはりO(n)の時間で求めます．これを点 p の回りを一周するまで続けます．このとき重要なことは，一つの三角形を求めるのにO(n)の時間しかかかっていないことです．一つの点に関する計算に n の2乗に比例する時間がかかってしまうことはあり得ますが，全体で三角形の個数が高々 n 個しかないことを考えると，全体の計算時間は n の2乗で抑えられることも分かります．
　この定数作業領域アルゴリズムの利点は，とにかくアルゴリズムが簡単であること，複雑なデータ構造が必要でないこと，作業領域は変数を少し用意するだけで十分であること，などです．実際にC言語のプログラムも書いてみましたが，全体でも200行程度の短いものです．実行時間は n の2乗に比例しますが，n の値が極端に大きな値でなければ十分に高速です．
　
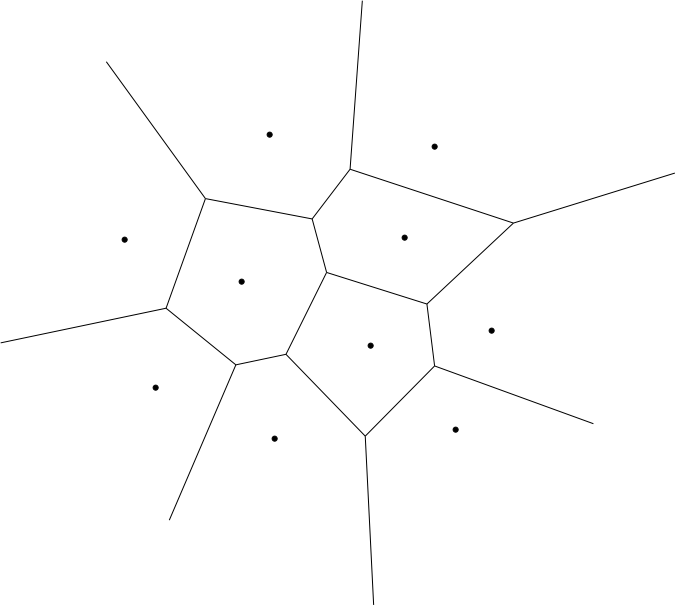
　デローネイ三角形分割を求めることができれば，その双対であるボロノイ図を求めることも簡単です．平面上の点集合Sに対するボロノイ図とは，平面をSのどの点に最も近いかという関係で分割したものです．下に示したのは，上と同じ点集合に対応するボロノイ図です．中央付近の点は多角形で囲まれていますが，その多角形内にどんな点をとっても，その点から最も近いSの点というのは，その多角形の内部にある点です．よく見てみると，ボロノイ図を構成する辺というのは，どれもSの2点の垂直2等分線になっていることが分かるでしょう．ボロノイ図は様々な形で応用されています．実際，ボロノイ図だけに関する国際会議も毎年開催されているほどです．
　実はデローネイ三角形分割とボロノイ図は双対という関係にあります．すなわち，ボロノイ図において，点 p を含む多角形と点 q を含む多角形が辺で隣接しているなら，しかもそのときに限り，2点 p, q を結ぶデローネイ辺が存在するという関係があります．したがって，どちらかを求めるアルゴリズムがあるなら，それを他方を求めるアルゴリズムに改変することは難しくありません．

　利用できるメモリに制限がある場合についてアルゴリズムを考えるという研究は始まったばかりです．ですから，新たな問題を見つけることも比較的容易であろうと考えています．また，上では定数作業領域のアルゴリズムしか述べませんでしたが，作業領域と実行時間の間のトレードオフを考えることも重要です．たとえば，n個の数値が与えられたとき，O(n)の作業領域を使ってよいなら，O(n)の時間で中央値（大小順に並べたとき中央にくる値）を求めるアルゴリズムが知られています．では，k 個の変数しか作業領域として使えないときはどうかというと，n の1+1/k乗に比例する時間で中央値を求めるアルゴリズムが知られています．このように，一般に大きな作業領域を使えば高速に問題が解けますが，実行時間との兼ね合いを調べるのがトレードオフに関する研究です．これも始めたばかりで，余り多くの結果は得られていません．