人間は音声を知覚する場合、音声信号から巧みに特徴を抽出し、利用している。しかし、この過程を機械に行わせようとすると、様々な問題が生じる。例えば、連続音声の生成過程において、前後の音韻から影響が及ぼされる調音結合がその一つである。
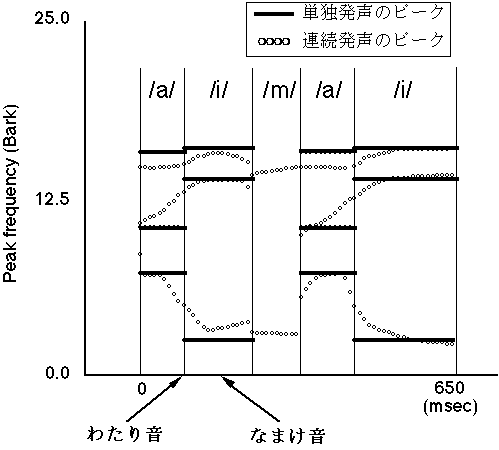
連続音声中では、ある音韻を発話する際その音韻の調音の目標まで達しないうちに次の音韻の発話に移る。従って、実現された音響的特徴は、単独で発話されたときの音韻固有の音響的特徴に達していない(なまけ音)。また、連続的に変化するために特徴が完全でない部分が生じる(わたり音) (図3)。機械はこのような音韻が不完全な部分を誤認識してしまう。しかしながら、人間には不完全な音響的特徴から目標値の推定を行なうという知覚機構が存在すると言われている。従って、この機構がモデル化ができ、これを認識装置に組み込むことができれば認識率の向上が期待出来る。そこで、補正機構の一つと考えられているーゲット予測と文脈効果のモデル化について次説で考える。

1.1 わたり音の回復 −ターゲット予測−[1]-[4](研究期間:1984 - 1989)
調音結合からの補正機構のモデルの一つとして、心理学的知見のみならず聴覚末梢系の知見を取り入れたターゲット予測モデルが提案されている[1][2]。
モデルでは、補正は「聴覚系内に音韻ターゲット予測機構が存在し、この予測値を人間は知覚している」ために生じると仮定し、この機構を計算機上に実現している。モデル化にあたって用いた知見および手法は次のものである。
Klattが提唱した聴覚末梢系の工学的モデルのうち、
(1) 有毛細胞をモデル化するための半波整流器
(2) ラウドネス尺度近似のための対数変換
(3) 基底膜をモデル化するためのメル尺度
(4) 側抑制をモデル化するための周波数領域での重み付け
を採用している。また、心理学的知見として
(1) 人間はホルマントの変化だけではなくスペクトル全体の変化を聴いている
(2) スペクトル変化極大点が前出音と後続音の知覚を分ける時点である
(3) 変化量と変化速度には相補的関係がある
(4) 予測には短い時間(約50 ms)の時間幅の情報だけを用いる
さらに、音声生成側からの制約として
(1) 音声の物理的特徴量の変化は臨界制動二次系で近似できる
を用いて、次式によりスペクトルの変化を記述している。
![]()
ここで、![]() は時刻
は時刻![]() のスペクトル、
のスペクトル、![]() はスペクトルの変化、
はスペクトルの変化、![]() はフィードバック係数、
はフィードバック係数、![]() は変化時定数である。
は変化時定数である。
上式において![]() とすれば、臨界制動二次系となり、一般解は
とすれば、臨界制動二次系となり、一般解は
![]()
となるので、この式の![]() が推定できれば、ターゲットの予測が可能となる。文献[1]では、
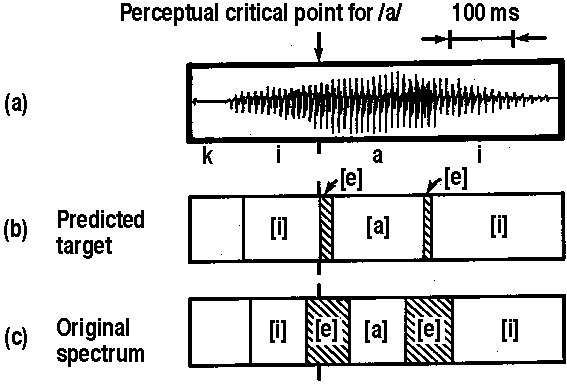
が推定できれば、ターゲットの予測が可能となる。文献[1]では、![]() の推定を指数関数のパラメータ推定問題に置き換えることによって、短時間の情報だけでターゲットを予測している。結果の一例を図4に示す。音声/kiai/において、わたり音である[e]の時間幅が減少していることがわかる。筆者はこの研究[1]で電子情報通信学会論文賞を受賞した。
の推定を指数関数のパラメータ推定問題に置き換えることによって、短時間の情報だけでターゲットを予測している。結果の一例を図4に示す。音声/kiai/において、わたり音である[e]の時間幅が減少していることがわかる。筆者はこの研究[1]で電子情報通信学会論文賞を受賞した。
ターゲット予測モデルは音声認識装置の前処理としても有効であり[3][4]、線形判別のための前処理[3]、あるいは、LVQのための前処理[4]として有効に働く。
1.2 なまけ音の回復 −文脈効果モデル−[5]-[8](研究期間:1988 - 1996)
音響レベルでの文脈効果モデルとして、心理物理実験から得られた知見を基に、スペクトルピーク間の相互作用による文脈効果モデルが提案されている[5][6]。モデルは、「音響レベルの文脈効果はスペクトルピーク対の相互作用の和としてモデル化できる」ことを仮定して、次式により定式化されている。
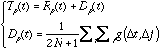
ここで、![]() :単独発話した場合のスペクトルピークの周波数、
:単独発話した場合のスペクトルピークの周波数、![]() :連続発話した場合のスペクトルピークの周波数、
:連続発話した場合のスペクトルピークの周波数、![]() :スペクトルピークの知覚的移動量、
:スペクトルピークの知覚的移動量、![]() :サンプリング数である。また、
:サンプリング数である。また、![]() は相互作用関数と呼ばれ、時間
は相互作用関数と呼ばれ、時間![]() 、周波数
、周波数![]() 離れたスペクトルピークから受ける知覚的影響量を規定している。そして、その値はモデルの定式化において極めて重要である。なお、ここで用いる周波数は人間の聴覚特性を考慮したERB
rate[24]である。
離れたスペクトルピークから受ける知覚的影響量を規定している。そして、その値はモデルの定式化において極めて重要である。なお、ここで用いる周波数は人間の聴覚特性を考慮したERB
rate[24]である。
![]()
相互作用関数は、現在までに、心理物理実験による推定[5]-[7]、および![]() を
を![]() にできるだけ近付けるという規範の下での一般逆行列による推定[6]により得られているが、これらの関数が調音結合のある音声の認識に有効である保証はない。そこで、相互作用関数をスペクトルピーク間の相互作用だけではなくスペクトル全体に拡張し、次に示すように、最小分類誤り学習の理論を用いて認識誤りが最小となるように決定する[8]。
にできるだけ近付けるという規範の下での一般逆行列による推定[6]により得られているが、これらの関数が調音結合のある音声の認識に有効である保証はない。そこで、相互作用関数をスペクトルピーク間の相互作用だけではなくスペクトル全体に拡張し、次に示すように、最小分類誤り学習の理論を用いて認識誤りが最小となるように決定する[8]。
第1段階として、学習時の計算量の軽減および過学習の防止のために、相互作用関数を簡単な形式で近似する。これまでの研究から、スペクトルピークによる文脈効果は、
(1) 時間差![]() が小さいスペクトルピークからは同化効果を受け、時間差が大きいスペクトルピークからは対比効果を受ける
が小さいスペクトルピークからは同化効果を受け、時間差が大きいスペクトルピークからは対比効果を受ける
(2) 時間差が非常に小さい或は非常に大きいスペクトルピークから受ける文脈効果は小さいと考えられる。これらのことを踏まえ、相互作用関数を
![]()
ただし、![]() および
および![]() では
では![]() 、という形式で近似する。
、という形式で近似する。
第2段階として、連続発話データの母音中心のスペクトルをモデルにより変形し、変形後のスペクトルと単独発話の母音のスペクトルとのユークリッド距離を識別関数として、補正後のスペクトルを識別する。次に、最小分類誤り基準に従い、式の係数![]() から
から![]() の値を学習することにより、識別誤り率が最小になるような相互作用関数を求める。
の値を学習することにより、識別誤り率が最小になるような相互作用関数を求める。
結果を次式に示す。
![]()
相互作用関数の学習結果は、周波数の差が5 ERB Rateのスペクトルピークから受ける影響が最も大きい、また時間差が50 msec以内では同化効果、50 〜 150 msecでは対比効果が優勢であることを示している。これらは、心理実験から得られた結果[5][6]とほぼ一致する。
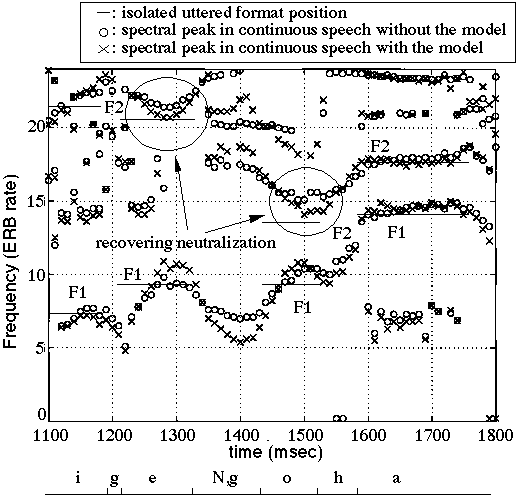
モデルによるスペクトル変形の効果を確かめるために、連続音声中のスペクトル系列に対してモデルを適用した(図5)。この図は怠けているスペクトルピークの軌跡が単独発話時のピーク位置に近づいていることを示している。また、モデルにより変形を加えた連続音声中の母音中心(最もなまけが大きいと思われる部分)のスペクトルと変形を加えていないスペクトルの識別率の違い、およびワードスポッティングの前処理としてモデルを用いた場合のスポッティング率を調べた。この結果、モデルを用いた場合に有意な性能の向上が認められた[8]。