列挙アルゴリズム合宿＠伊香保温泉

群馬大学伊香保研修所

群馬大学は、伊香保、草津、北軽井沢に宿泊施設を持っています。 特に、伊香保研修所は、学生向けの便覧等には掲載されていないのに、 他の施設に比べてとっても豪華です。 教員である私が、口コミでその存在を知ったのは、群馬大学に赴任して3年も たってからのことでした。

この伊香保研修所は、元々、皇室の別荘であったところを、 群馬大学に払い下げとなったものなのだそうです。 建物は火災等で消失したため、昔の面影は全くありませんが、 場所は、伊香保の一等地。さらに伊香保の温泉の権利の4分の1を もっているということで、温泉も一級品です。

格安な料金(5000円ほど)で朝夕2食つきで宿泊できます! 通信カラオケも充実! 管理人は、夕食の準備の後、自宅に帰ってしまうので、あとは、騒ぎ放題、 いやいや、白熱した討論のしほうだいという、 研究合宿には最適な場所なのです。

惜しむらくは収容人数です。 4-5人部屋が4つと、2人部屋が3つで 最大25名までしか宿泊できません。 けど、ひとつのテーマでの勉強会には、丁度いい人数かもしれませんね。

列挙合宿

この伊香保研修所にて、これまで3回、列挙アルゴリズム 合宿を行なってきました。

NIIの宇野先生がプログラム関係を, 群馬の中野が事務関係を担当しています。

事前にプログラムをキチンと決めず、当日、発表したい人から順に発表します。 通例の発表30分討論10分というようなシバリは全くありません。 ところが、 このような形式でも、発表者がいなくてとぎれてしまったことは、ありません! オレまだ発表してないよー! というほうは幾件かあります。 大幅に脇道でズレていくこともしばしばあります。 活気と熱意にあふれた、熱い討論が繰り広げられます。 ちなみに、名前は``列挙アルゴリズム合宿''ですが、 列挙に関係ない発表も大歓迎なのです。

第一回は2004年の4月に1泊で(4大学11名参加), 第二回は2004年の8月に2泊で(10大学19名参加), 第三回は2005年の3月に2泊で(12大学20名参加)と充実しつつあります。 第三回は、特定研究のミニ集会も兼ねています。

プログラムや当日の写真等は、ここから見ることができます。 ちょっと宴会の写真が多いかもしれませんが、 これは勉強会の最中は写真を撮るのもわすれて議論に没頭していたためです。

温泉効果

この合宿を、細く長く続けていけたら! というのが参加メンバーの願いです。 とはいっても、まだ、太くなるゆとりはありますので、 興味をもたれた方、ぜひ参加されませんか？ きっと、昔のスポコン漫画のような熱き心を思い出すことでしょう。

また、群馬の伊香保のお湯は, 研究推進に効果があるみたいです。 苦しいこともイヤなことも、お湯に流してしまいましょう。 最近、U野、U原、O本各先生あたりが元気なのも 伊香保温泉の効果によるという説もあります。

みなさまの研究推進にも、少しでもお役に立てますよう、 ぜひ、伊香保研修所でたくさんの研究会を開催できたら。。。と思います。 どうぞ、声をかけて下さい。 ちなみに群馬大学関係者のみでの予約は、ほぼ不可能なのです。 学外の人が沢山参加する研究会に対しては、予約を優先してもらえるのです。 伊香保で研究しましょう!

(2006年5月のアルゴリズム研究会は伊香保研修所で開催予定です。)

おまけ パズル

下記は、小学生の息子と一緒に某所で作ったものです。 真中の四角は竹を30センチほどに切ったものです。 竹の円筒形を横から見ています。

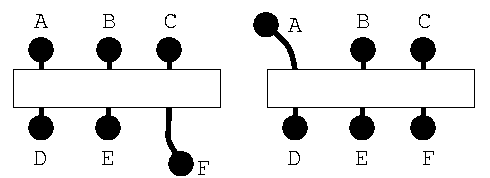
これに図のように6個所の穴があり、ここから、ひもが出ていて その先に球形の取手(とって)がついています。ひもは伸び縮みしません。 竹には見掛け上、変な細工はありません。 ひもの通る穴があるだけです。 ふしが両端にあるので、中身は見えません。

さて、左図で、球形の取手のヒモは1個所Fだけ伸びていますね。 他の5個所の球形の取手のヒモは竹の中におさまっています。

父

さてと、今、Fが伸びているよね。 さて、どれかのヒモを引くと、 Fがひっぱられるのだけど、どれかな？

子

えーと! A!

父

さーてとどうかな...(Aのひもをひくと、Fがひっぱられて、Aが伸び、Fは 竹にくっついた状態になります。右図参照) おー! (拍手)よくできたねー。

では、こんどは、Aが伸びているよね。どれかのヒモを引くとAが、ひっぱられるの だけど、どれかな？

子

えーと! B!

父

さーてとどうかな...(Bのひもをひくと、Aがひっぱられて、Bが伸び、Aは 竹にくっついた状態になります。) おー! (拍手)よくできたねー。

では、こんどは、Bが伸びているよね。どれかのヒモを引くとBがひっぱられるの だけど、どれかな？ 今度は、お母さんどうぞ!

母

えーと! A!

父

ホントにAでいいの! 残念でした。正解はC です。 ホラCを引くと、。。。。(Cが伸びて、Bがひっぱられて竹にくっつく。)

こんな感じで、子供の予想は全問正解、母の予想は全問不正解のように、 いくらでも続けられます:-)
実は、どの球形の取手を引いても、伸びている取手がひっこみます。 子供の予想に対しては、予想の取手を引き、 母の予想に対しては、予想でない取手を引き、こちらが正解であるかのように 話を続けます。。。。(あまり長くすると怒られますので注意!)

クイズ1:

さて、この機器のシカケは、どうなっているでしょう？ すなわち、6個所のうち、任意の1個所の取手が伸びている状態で、 残りの5個所のうち、どの1個所を引いても、伸びているものがひっこむのです。 変なシカケはありません。ヒモのカラミ方だけが問題なのです。

クイズ2:

今回は6個所に取手がついていますが、これを2n個所に一般化して下さい。

どなたか、このパズルの名前を知っていませんか？

実物をさわると、パズルごころが、ふるえますよ。 群馬に来たおりには、ぜひ、さわっていって下さい。

Back to Table of Contents Last modified: Wed Jul 20 16:54:42 JST 2005 modified/maintained by R.Uehara (uehara@jaist.ac.jp)