[English/Japanese]
複数の箱を作ることができる展開図
ここは「2つの異なる箱を作ることができる展開図」を公開しているページです.
たとえば以下の図を見て下さい.
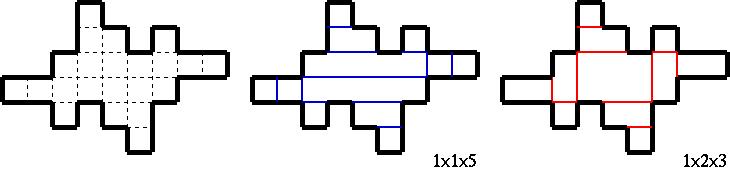
左端の展開図は,中央の青い線にしたがって折ると,1×1×5のサイズの箱ができますが,
右の赤い線にしたがって折ると,1×2×3のサイズの箱ができます.
表面積は同じで,体積が違うところがポイントです.
最近読んだ本
「Geometric Folding Algorithms: Linkages, Origami, Polyhedra」
(by Erik D. Demaine and
Joseph O'Rourke)
の図25.53にこうした性質の展開図が2つ描かれています.
これ以外にもこうした展開図はないだろうか,と思ったのがこの研究の発端です.
今のところ,こうした展開図が2000個以上あることがわかりました.
(2008年8月現在,9000個以上(!!)あることがわかりました.
以下のCCCG 2008の
予稿の長いバージョンに詳細が書かれています.)
本研究については,以下のところで発表しました.それぞれで使用した原稿などを公開しておくので,
詳細はそこを御覧下さい.
- Gathering for Gardner(マーチン・ガードナーを囲む会)

- 2010年3月24日〜28日にアトランタで開催されたG4G9で
この展開図を紙のパズルとして製作したものを配布しました.
私が選んだパズルとしての展開図のパターンを公開(PDF,
EPS)しておきます.これらはパズルとしてかなり楽しめます.
実際のパズルは右の写真の通り,1mmの凸凹や折りのための切れ込みがつけてあり,
折った部分が噛み合って自立するようになっています.
パズルの製作は東京紙器さんにお願いしました.
とても精巧な加工をしてくれるので,とても助かりました.
- 第4回折り紙の科学・数学・教育 研究集会
- 2008年6月22日(日曜日)の朝一番の発表です.
無事に発表が終わりました.
当日使ったパワーポイントのファイルを置いておきますので,
興味のある方はどうぞ.
- The 20th Canadian Conference on Computational Geometry (CCCG 2008)
- 2008年8月13日〜15日の期間,カナダで開催された国際会議です.
8月13日の朝に発表が無事終わりました.
予稿には短いバージョンと
長いバージョンがあります.
英語なのですが,図が多いので許して下さい.
以下の各ページでは,面積別に展開図の一覧を表示しています.
展開図として有効なのか無効なのか,微妙なものがあるのですが,
判断基準は次の通りです.
- 角がくっついているとき
- これは有効です.角でつながってるだけなら,大丈夫です.
次に例をあげておきます.



































- 辺がくっついているとき
- 箱を組み立てるときに,辺を切らないといけない場合です.
ここではこれは無効と判断しています.
一般に2つの別々の箱を作るためには違う辺を切らないといけないので,
これはいけないだろうと思っています.
解答の中にはもしかしたら「同じ辺を切ると別々の箱ができる」
パターンもあるかもしれませんが,チェックしていません.
次に例をあげておきます.










































- 四角形が重なっているとき
- 箱の一部の四角形が重なっている場合です.以下の例では,面積22のはずなのに,
四角形が21個しかありません.つまり重なりがあります.
しかも2通りの組み立て方では,一般に重なっている部分が違います.
これは有効な展開図とは言いにくいです.



































なお,上記の「無効な展開図」をプログラムでチェックしてはじくことは簡単です.
具体的には
- 四角形の数を数えて,足りないものは無効
- 内部に穴の空いているものは無効(これは外周をぐるりと回って面積を調べて,
想定している面積と比較すればすぐわかります.)
とすれば効率良くはじくことができます.
今回それをやらなかったのは「はたしてこういうパターンはどれくらいの頻度で現れるのだろう」
という興味があったからです.正しい展開図2136個に対して無効な展開図29個ですから,
かなり少ないことがわかりました.
- 面積22のとき
- 正しい展開図:538個, 無効な展開図18個; すべての展開図
[追記]
2011年3月に松井寛彰くんが面積22のケースの全探索に成功しました.
面積22の展開図で1×1×5と1×2×3の両方の箱が折れる展開図の個数は2263個
あることがわかりました.すばらしい.
本当の意味でのすべての展開図も公開します.ただしデカいので要注意です.
- 面積30のとき
- 正しい展開図:72個, 無効な展開図1個; すべての展開図
- 面積34のとき
- 正しい展開図:708個, 無効な展開図0個; すべての展開図
- 面積38のとき
- 正しい展開図:41個, 無効な展開図0個; すべての展開図
- 面積46のとき
- 正しい展開図:660個, 無効な展開図8個; すべての展開図
- 面積54のとき
- 正しい展開図:3個, 無効な展開図0個; すべての展開図
- 面積58のとき
- 正しい展開図:37個, 無効な展開図0個; すべての展開図
- 面積62のとき
- 正しい展開図:5個, 無効な展開図0個; すべての展開図
- 面積64のとき
- 正しい展開図:56個, 無効な展開図2個; すべての展開図
- 面積70のとき
- 正しい展開図:14個, 無効な展開図0個; すべての展開図
- 面積88のとき
- 正しい展開図:2個, 無効な展開図0個; すべての展開図
- 合計
- 正しい展開図:2136個, 無効な展開図29個.
なお,それぞれの展開図からどうやって2通りの箱を作るのか,という具体的な折り方は,
このデータには入っていません.パズルとして,簡単なものからかなり難しいものもありますので,
そこはお楽しみ下さい :-)
[追記]
2008年8月11日に伊藤剛志さんが
上記の展開図の中に3通りの箱を折ることのできる展開図がないかどうかを
プログラムでチェックしてくれました.結局見つからなかったそうです.
また,面積22のときの無効な展開図は当初は15個と書いてあったのですが,
正しくは18個でした.ご指摘どうもありがとうございます.
Last modified: Thu Aug 21 13:47:40 JST 2008
by Ryuhei Uehara (uehara@jaist.ac.jp)
| 
|

















































































































