三上・山上・参上・三乗？

はじめに

研究者とは，二つのものを思いつかなければならない． 一つは「問題」であり，もう一つは「解」である． したがって，よい研究者というのは「よい問題」や「よい解」を思いつく人であろう． ではこうした「よい問題」や「よい解」は，どういうときにヒラメクのだろう． 私は必ずしも「よい問題」や「よい解」ばかり思いついたわけではないけれど， 「変わった問題」や「変な解」は，わりと思いついているように思う． 特に最近は，例えば「飛び出す絵本はNP困難」とか，「じゃばら折りを高速に作るアルゴリズム」とか， ぱっと見るとマッドサイエンティストになっちゃったのかと 誤解されかねない（今回の夏のLAでも「折紙の計算不能問題」という， かなりマッドサイエンティストのニオイが漂う話をしようと思っている． 念のために言っておくと，計算モデルに関するわりと真面目な話(?)である．）研究に，わりとハマっている． せっかくのチャンスなので，こういう「変」なことをどこで思いつくのか，秘訣をこっそりとお教えしよう． もちろんそれで「よい」研究者になれるかどうかは，保証の限りではない．

どこで思いつくのか

古来，文章を練るのにもっともよく考えがまとまるという場所が三つあり， 「三上」と呼ばれている．具体的には，厠上・枕上・馬上である． 要するにトイレに入っているときと，寝ているときと，馬に乗っているときである．

私はトイレにはあまり長居しない．だいたい当面の問題を解決するのに忙しくて， 考えごとをしているヒマはない．そんなわけで，私の場合には「厠上」は，あてはまらない． でも washroom と連想を広げると，風呂を代わりにつけ加えたい． 風呂の中では，よく問題を考えていたり解を考えていたりする． ときにはとてもよいことを思いつくこともある． もしかしたら「三上」の「厠上」の厠には，風呂も入っているのかもしれない．

図１：Super IQ．一見，簡単そうだが
とてつもなく難しい．
解けない人は何ヶ月やっても解けない．
でも解けると，とてつもなくうれしい．

次の「枕上」には，かなり同意できる．私はよく考えごとをしながら寝入ってしまい， 夢の中で問題が解けることがある．ときにはガバっと起き上がって，書きつけて， それから寝ることもある．そういうメモは次の日に見ると，大抵何が書いてあるかわからない． たとえわかっても，だいたい間違っている．しかしごくまれに，ヒットすることもある． 以前，Super IQ と呼ばれるパズルをやったときのことはよく覚えている（図１）． これは，[1×1×1のブロック5個]と[1×2×4のブロック6個]と [2×2×3$のブロック6個]を5×5×5の箱に納めるパズルである． 単純な構成なのに，とてつもなく難しい．是非やってみてもらいたい． 私は夕方に１時間くらいやって挫折して放りだし，ふてくされて寝てしまった． そして夢の中でああでもないこうでもないと考えていたら，突然，解答を思いついた． とても印象的な解だったので忘れるはずもなく，次の日の朝は， ただその解答の正しさをチェックするだけだった．

さて最後の「馬上」である．最近は馬で通勤・通学する人も珍しいだろうから， これが当てはまる人はなかなかいないと思われる． そこでお薦めしたいのが「自転車上」である．私は金沢市内からJAISTまで， 片道18km程度の道のりを自転車通勤している．（もちろん天気が悪いときはいさぎよくあきらめる．） この上で私はよく考えごとをしている．車やバイクだと危険なのでお薦めしないが， 自転車だと，わりと考えごとができる． 体を動かして汗をかいているので血のめぐりもよく，また頭はヒマなので，考えごとに向いているのだと思う． 余談だが，ローラー台の上で自転車を漕ぎながらアクションゲームをやると， 普段よりもずっと簡単にゲームをクリアできるそうだ．たぶん新陳代謝が高まっているので， 反射神経も鋭くなっているのだろう．「どうしてもあの面がクリアできない」と 行き詰まっている人は，覚えておくとよいだろう．

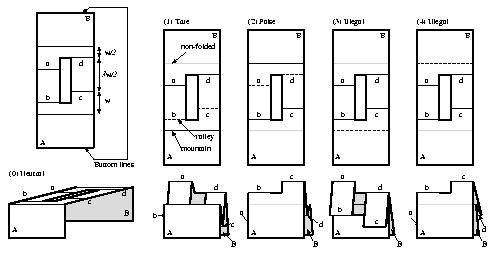図２：変数ガジェット．

それはさておき，自転車上での考えごとである．もちろん複雑な計算はムリなので， もっぱら図的な考察に限るような気がする．私の場合は，還元のガジェットを 考えている場合が多いと思う．例えば「飛び出す絵本はNP困難」という結果を出した[UT09]とき， 鍵となるガジェットは図２に示したものである． これは図中(0)で示したニュートラルな状態からの折りたたみかたが本質的に二通り((1)と(2))あって， それぞれが true と false に対応する．（ちなみに(3)と(4)は別のガジェットの影響で折れない．） 図に示した通り，折り線はとても単純であり，ちょっと考えれば，誰でも容易に理解はできるだろう． しかし自分でこれを思いつけるかというと，かなりの人が「う〜む」と思うだろう． いま自分で見てもそう思うくらい，これはよくできている． このガジェットは自転車の上で思いついたものである． しかもよほど印象的だったと見えて，数年前のできごとにも関わらず， いまだに「思いついた交差点の場所」まで，よく覚えている． こうした強烈なアイデアは，メモをとらなくても忘れることはないようだ． この論文では，ほかにもいくつかの興味深いガジェットがあるが， その多くは自転車上で思いついていて，まさに自転車通勤の賜物である．

図３：一見不可能に見える折紙．
作りかたはもちろん秘密である．

さて，最近の私は出張が多い．そこで割り切って「ユビキタスリサーチャー」を目指している． （ユビキタスリサーチャーとは「研究のあるところなら，どこにでも遍在する研究者」と定義される． 今のところ最遠は，たぶんバルバドスだと思う．） そのため「機上の人」「車上の人」である時間が長い． こうしたところも逆に割り切ると，研究の場としては悪くない． なんせ電話がかかってこない（私はいまだに携帯電話は持っていない）し， 学生が質問にも来ないので，割り込みがかからない． 「機上」ならば，呼ぶだけで飲物までサービスしてくれるのだ． 欠点は論文などを一生懸命読むと，乗物酔いすることであろうか． しかし最近の私は「折紙の研究」をしているので，紙切れをいじっていると研究になるという利点がある． 最近の例でいえば，半年くらい解けていなかった「n個の等間隔の折り目のついた紙の， 異なる折りたたみ方法の個数の指数下界」[Ueh10b]の証明方法を， 「飛行機がハワイに着陸した瞬間」に思いついた（ちなみに2009年のISAACである）． 着陸後に滑走路を走っている間，隣の席でそれを無理矢理語られた妻や， ハワイのホテルで会うなりいきなりそれを語られた電通大の山中さんには，ちょっとだけ悪いことをしたかもしれない． また，「一見不可能に見える折紙」（図３）を思いついたのは， ERATOのキックオフミーティングに参加するために北海道に向かう飛行機の中である． これまた，無理矢理試作品を見せられるはめになった東海大の松井さんや， NIIの宇野さんにはちょっとだけ迷惑をかけたかもしれない．

図４：カメラ目線の特別天然記念物．
（本当に上原撮影）

以上をまとめると，だいたい「手ぶら」で時間があって「頭がヒマ」な状態のときが， アイデアを得るための重要なファクターであるように見える． しかし必ずしもそうとばかりは言えないところが悩ましい． 私の場合，例えば「ヒマな会議」のときには，条件は満たされているのだが，あまりいいアイデアが浮かばない． そういう意味でも会議は少ない方がよい． また私は山登りや，ときには自転車で山登りをすることがある． （今まで自転車に乗っていて，犬・猿・キジはもとより， ニホンカモシカ，タヌキ，ウサギなどなど，いろんな野性動物に遭遇した． 特別天然記念物であるニホンカモシカとは，3mくらいの至近距離でしばらく見つめ合ってしまった（図４）． 幸い，まだ熊には会ってない．） そのときも山上に参上したらアイデアが三乗というわけでもない． わりと普通である．さすがにここまで状況がシビアになると，研究に頭が回らないのかもしれない． 山登りが大好きな京大の岩間先生は，やはり山でアイデアを思いつくのだろうか．

どうやって思いつくのか

さて三上については，もうよいこととしよう． しかしここで，無い袖は振れないということを忘れてはいけない． 頭が空っぽでは研究のしようもない．頭の中に普段から素材を貯めておくことも重要だと思う． 特に「新しい問題を考える」というのは，問題を解くのとは別の意味で難しい部分がある． なんら新しい素材を蓄えることなくして，新しい問題を思いつくことは難しいだろう． もちろん机に向かうことがもっとも重要であることは言うまでもないが，私の場合は， 手と足を積極的に使って素材を集めているように思う．

まず「足」である．「最近出張が多い」と上で書いたが，いろいろな国際会議に行くことにしている． 最近は「数人のグループで書く論文」が増えている． ここでいうグループとは，同じ大学の教授・准教授・助手・学生といった階層的なものではなく， いろいろな大学の同レベルの研究者グループをさしている． こうしたグループで上手にコラボレーションすると，単なる人数分以上のものをもつ論文が生まれる． もちろん自分の名前の入った論文の数もぐっと増える．しかしこうしたグループは一朝一夕でできあがるものではない． いろいろな機会に少しずつ自然発生的に生まれていくものである． こうしたグループにうまく入り込むには，やはり足が必要であろう．前回のLAの会誌で 電通大の山中さんが「伊香保温泉の列挙合宿」を取り上げていたが，こうした機会を見つけて， 積極的に生かすことが大切であろう．

図５：おばけ煙突．見る方向によって本数が変化する．

そんな機会の一つとして，最近バルバドスに行った． バルバドスにはカナダ・モントリオールの McGill 大学の保養施設があり（「なぜ McGill の施設がバルバドス にあるのか」という理由も面白いが，ここでは省略する．）， 2010年2月にここで１週間ほど合宿形式でこってりと議論をした． その結果の一部は[CDD+10b]や [DDU10]として結実している． このときの参加者は20名前後で，とても密度の濃い充実した合宿であった（日本人は（たぶん島中含めて）私一人であった）． ちなみに論文[CDD+10b]の タイトル``Ghost Chimney''とはいわゆる「おばけ煙突」で，昭和39年まで足立区に存在した煙突である． こう書くと，またマッドサイエンティストに一歩近づいているように見えるが，そうでもない． 「おばけ煙突」は，見る方向によって本数が１本〜４本まで変化する（図５）． こうした配置の一般化を議論したものである．詳しくは論文を参照してもらいたい． なお，この論文を書くにあたっての資料写真を足立区郷土史料館にいただくなど（図５もその一部である）， いろいろと面白い体験も味わうことができた．

図６：不可能物体．
これはもはや博物館級．
一番下には「５円玉に
木の矢が刺さったもの」
が入っている．もちろん
ビンの口は５円玉より細い．

そして「手」である．私の部屋には，おかしなものがたくさん転がっている． パズル（図１）や不可能物体（図６）や折紙（図３）などである．いろいろと集めたものもあり， 偶然手に入ったものもあり，執念で手に入れたものもあり，勝手に集まってきたものもある． もちろん自分で作ったものもある． こうしたガジェットは，普段から頭を軟らかくすることにも役にたつかもしれないが， ときには本当に論文を書くのに役立つこともある． 例えば「飛び出す絵本はNP困難」という結果を出した[UT09]とき， 「完全に閉じた状態から，開きかたが２通りあるガジェット」を作る必要があった． このときのガジェットは，昔からあるおもちゃ「パタパタ」のメカニズムをそっくりそのまま使って実現した． 例えば不可能物体にしても，これを作り出すには，なんらかの「アルゴリズム」が存在するはずである． みなさんは図３に潜むアルゴリズムや， 図６に潜むアルゴリズムを見破ることができるだろうか． （「見破った」という人は，同じものを作って下さい．「原理的にはこれでできるはず」は「見破った」とは認めません :-)）

さて最後に「じゃばら折りを高速に作るアルゴリズム」の研究 [CDD+10a] の裏話を披露しよう．これは2009年の冬のLAで発表して「LA/EATCS発表論文賞」をいただいた論文である． 著者がたくさんいるのは，あちこちの研究会で発表するたびに，聞いた人が次々に結果を改善して参戦してくれたおかげである． そういう意味ではグループで書いた論文ともちょっと違う．個人的には， 2008年の CCCG の Open Problem Session でこの話をしたときに， あのロン・グレアム(Ron Graham)に「いい問題だねぇ」と褒められたことが忘れられない． また，このテーマは意外な広がりもあり， 派生した問題も別途論文になりつつある[Ueh10a][Ueh10b]． なかなかよいテーマであった． この問題を思いついたのは，実は自転車の上ではなくて，コンピュータのキーボードの前である． ある日「なんか純粋に『手間』だけが問題になる折紙の問題はないかなぁ〜」と考えながら， キーボードの前で紙切れをいじりながら，ふと思いついた問題なのである． まさに『手』で思いついた問題と言えよう．こういうタイプのヒラメキには，残念ながら説明できるコツはない．

おまけ

図７：ライブキューブ．これがあると
立方体が単位のものは大抵作れる．

図１に示した Super IQ は最近は入手が難しいようだ． でもこれは単純なピース構成のパズルなので，簡単に自作できる． 紙で作ってもいいのだが，こうしたパズルの自作に，とてもよいキットがある． それは「ライブキューブ」だ（図７）． これは立方体が単位のパズル類やポリオミノなどが簡単に作れるブロックである． 日本では２件しか扱っていない（パズラボと トリト）が，超お薦めである． これを使えば机上や，場合によっては機上でも，いろいろと手を使って考えることができる． もしかしたら，すばらしい問題や解が見つかるかもしれない． ただし指導教官に「遊んでいる」と叱られたり，マッドサイエンスにはまってしまっても， 責任は持てないのであしからず．

なお，本稿の図５の写真は，足立区の歴史博物館から使用許可をいただいた． また図６については， 「不可能物体ぎゃらりぃ」を管理されている kiyori さん本人から直接現物をいただいた．感謝します．ホントにうれしいです．

[CDD+10a] J. Cardinal, E. D. Demaine, M. L. Demaine, S. Imahori, T. Ito, M. Kiyomi, S. Langerman, R. Uehara, and T. Uno. Algorithmic Folding Complexity. Graphs and Combinatorics, accepted, 2010.

[CDD+10b] D. Charlton, E. D. Demaine, M. L. Demaine, V. Dujmović, P. Morin, and R. Uehara. Ghost Chimneys. In 22nd Canadian Conference on Computational Geometry (CCCG), pp. 63-66, 2010.

[DDU10] E. D. Demaine, M. L. Demaine, and R. Uehara. Any Monotone Function Can Be Realized by Interlocked Polygons. In 22nd Canadian Conference on Computational Geometry (CCCG), pp. 139-142, 2010.

[Ueh10a] R. Uehara. On Stretch Minimization Problem on Unit Strip Paper. In 22nd Canadian Conference on Computational Geometry (CCCG), pp. 223-226, 2010.

[Ueh10b] R. Uehara. Stretch Minimization Problem of a Strip Paper. In 5th International Conference on Origami in Science, Mathematics and Education (5OSME), 2010.

[UT09] R. Uehara and S. Teramoto. Computational Complexity of a Pop-Up Book. In Origami⁴, pp. 295-304. A K Peters Ltd, 2009.

Last modified: Fri Nov 12 23:33:06 JST 2010 by Ryuhei Uehara (uehara@jaist.ac.jp)