Part III:
Complex Dynamical Systems
as Metaphors
Putting Together:
mind
causality
depth
complexity
mechanisms
Lesson from Lecture One: The mind is
a causal system which has depth,
therefore, it is complex in a precise sense.
Lesson from Lecture Two, Part II.: Causal
systems are describable as mechanisms.
e.g. when looking for the mind we are looking
for a system (dynamical system) which
has depth and which supports mechanisms
.
Claim: chaotic itinerancies can
be metaphors of such dynamical systems.
Chaotic Itinerancy
I. Tsuda:
"In low-dimensional dynamical systems, the [asymptotic]
dynamical behavior is classified into four categories: a
steady state
, a periodic state
, a quasi-periodic
state, and a chaotic state
. Each class of behavior is represented by a fixed point attractor,
a limit cycle, a torus, and a strange attractor, respectively. However,
the complex behavior in high-dimensional dynamical systems is
not always described by these attractors. A more ordered but more complex
behavior than these types of behavior often appears. We [Kaneko, Tsuda et
al.] have found one such universal behavior in nonequilibrium neural networks,
globally coupled chaotic systems, and optical delayed systems. We called
it a chaotic itinerancy. "
"Chaotic itinerancy (CI) is considered as a novel universal class
of dynamics with large degrees of freedom. In CI, an orbit successively
itinerates over (quasi-) attractors which have effectively small degrees
of freedom. CI has been discovered independently in globally coupled maps
(abbrev. GCM), model neural dynamics, optical turbulence."
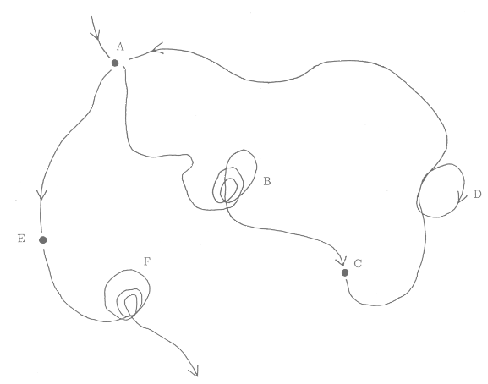
Figure: Schematic drawing of chaotic itinerancy.
Dynamical orbits are attracted to a certain attractor ruin, but they leave
via an unstable manifold after a (short or long) stay around it and move
toward another attractor ruin. This successive chaotic transition continues
unless a strong input is received. An attractor ruin is a destabilized Milnor
attractor, which can be a fixed point, a limit cycle, a torus or a strange
attractor that possesses unstable directions.
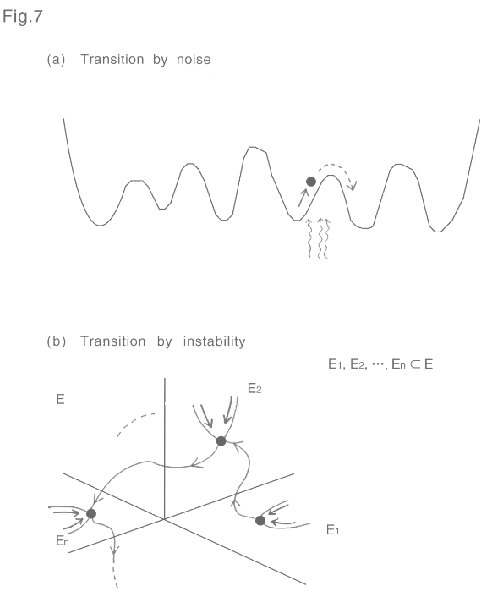
Figure: The difference between transitions created by producing
chaotic itinerancy and by introducing noise. (a) A transition created by
introducing external noise. If the noise amplitude is small, the probability
of transition is small. Then, one may try to increase the noise level in
order to increase the chance of a transition. But this effort is not effective
because the probability of the same state recovering is also increased as
the noise level increases. In order to avoid this difficulty, one may adopt
a simulated annealing method, which is equivalent to using an "intelligent"
noise whose amplitude decreases just when the state transition begins. (b)
A transition created by producing chaotic itinerancy. In each subsystem,
dynamical orbits are absorbed into a basin of a certain attractor, where an
attractor can be a fixed point, a limit cycle, a torus, or a strange attractor.
The instability along a direction normal to such a subspace insures a transition
from one Milnor attractor ruin to another. The transition is autonomous.
Recently, Komuro constructed a mathematical theory of chaotic itinerancy with
the same idea as demonstrated in (b) , based on the investigation of itinerant
behavior appearing in the coupled map lattices found by Kaneko (Komuro 1999).
K. Kaneko and I. Tsuda ``Complex Systems: Chaos and Beyond
-----A Constructive Approach with Applications in Life Sciences" (Springer,
2000)
K.Hashimoto and T.Ikegami,
"Heteroclinic Chaos, Chaotic Itinerancy and Neutral Attractors in
Symmetrical Replicator Equations with Mutations",
J. Phys. Soc. Japan. 70 (2001) pp.349--352.
How Far Can We Get?
CI-s show some kind of depth (what happens to the low-dimensional system
happens to the entire very high
dimensional system).
In order for CI-s to be interesting for supporting causality and mechanisms,
it should be possible to control them
efficiently, in specific ways. In particular, it should be possible to
use CI-s for defining low-dimensional systems
which give rise to other, well-defined, new low-dimensional systems, autonomously
or if triggered properly.
Is it actually possible to use CI-s in such a way? E.g. can we synthesize
finite automata on them?
Another, related question is this. Are CI-s complex enough? At this moment,
for me, this is very unclear.
My thinking goes backward. We want causality and depth, and we find CI-s
on the road. Clearly they are
superior to ordinary dynamical systems which have no depth and no causality
at all. But how good are they?
Is this already the most general kind of system you can get?
Using another metaphor (suggested in Lecture One), the "chemistry of
mind", and using the popular notion of
computation, one way of expressing our question is this: are CI-s able
to perform all computations (viz. causal
transitions) doable by chemical systems?

